“Bandit Algorithms” Tor Lattimore & Csaba Szepesvari の 輪読会の資料です。世界標準のバンディットの教科書なので、 世界標準レベルの入門記事と言えます。(過言)

第1章:イントロダクション
バンディット問題の源流は、William R. Thompson(1933)の論文です。Thompson は 臨床試験 に関心があり、その応用を想定してバンディット問題を考えました。
ただ、このときはまだ「バンディット問題」という名前はついていません。
この名前は、1950年代に、Frederick Mosteller と Robert Bush が動物の学習を研究し、マウスそして人間で実験を行ったことに由来します。
T字路のある迷路にマウスを置きます。T字路の端には食べ物があり、どちらの端で食べ物を見つけられるかをマウスは学習します。人間における同様の学習環境を研究するために、「2本腕バンディット」マシンが作られました。
人間はマシンの左腕か右腕のどちらかを引くことができ、それぞれの腕を引くと、プレイヤーには 未知の確率分布 で ランダムな報酬 が与えられました。このマシンは、昔ながらのレバー操作のスロットマシンになぞらえて、2本腕バンディットと呼ばれました。(バンディット=盗賊がお金を盗むからそう呼ばれる)
臨床試験が将来の重要な応用である一方で、バンディットアルゴリズムはすでに広く使用されています。大手テック企業は、ニュース推薦、動的価格設定、広告配置 などのウェブインターフェースを設定するためにバンディットアルゴリズムを使用しています。

また、Bandit Algorithm に対する注目度はここ最近上がっています。
「Bandit Algorithm」 を Google Trend で調べた結果👇
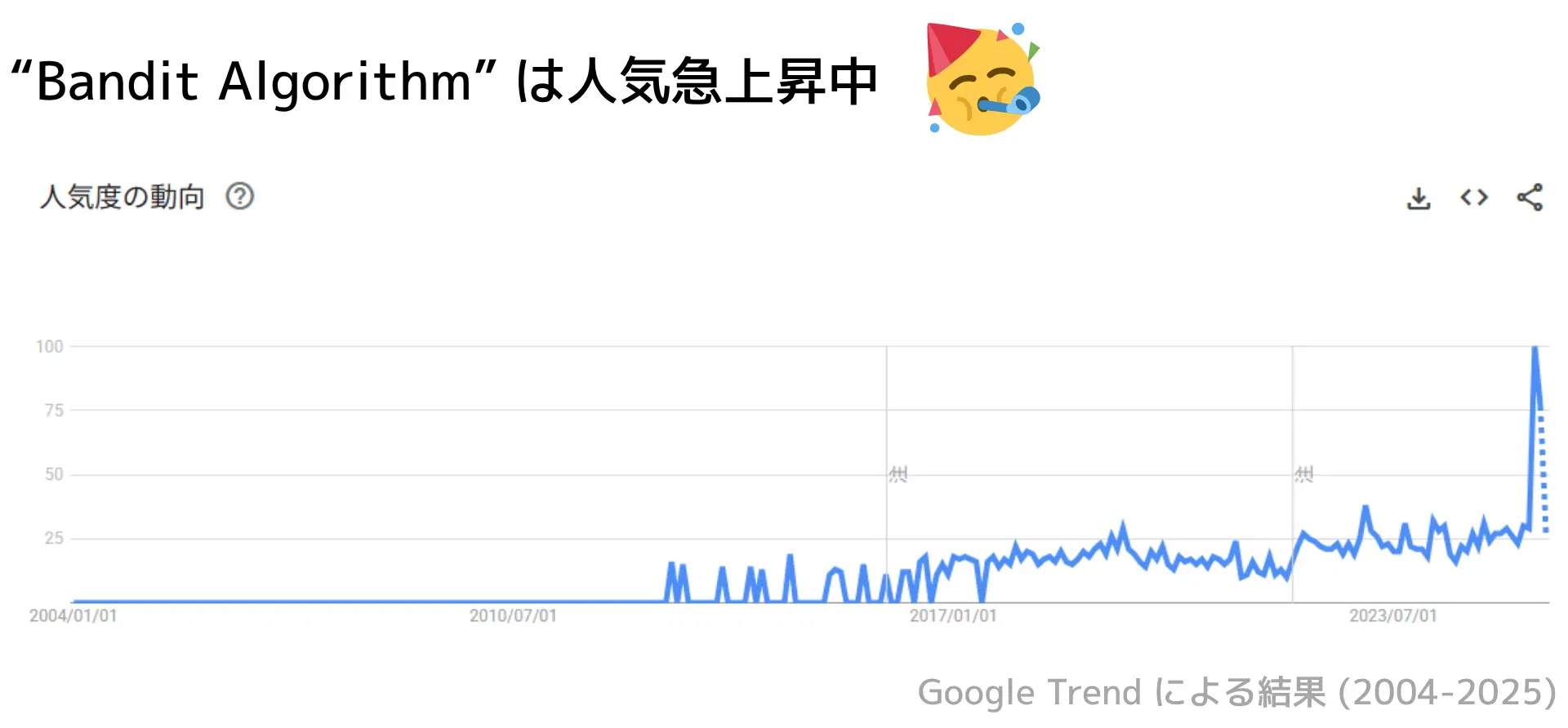


Bandit Algorithm は 不確実な環境で最善の選択を逐次的に意思決定するための方法 です。
たとえば、以下のような状況を考えてみましょう。
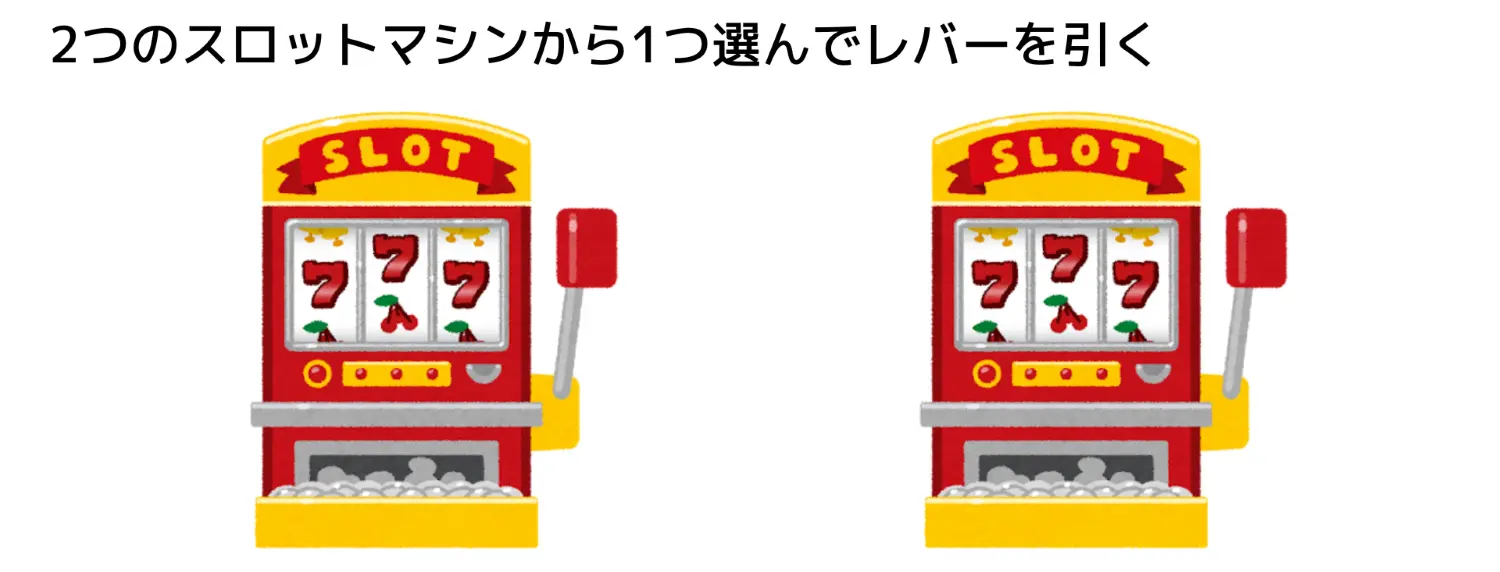
あなたが2本腕のスロットマシンをプレイしていて、すでに各レバーを5回ずつ引いた結果、以下のペイオフ(ドル単位)が得られたと想像してみてください。
| ラウンド | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 左腕 | 0 | 10 | 0 | 0 | 10 | |||||
| 右腕 | 10 | 0 | 0 | 0 | 0 |
左腕と右腕で平均ペイオフは?
➡ 左腕:4ドル、右腕:2ドル
左腕 の方がわずかに優れているように見えます。
こんな状況で、あなたはどのようにプレイしますか?
- 右腕のパフォーマンスが悪いことを無視して左腕を引き続けますか?
- それとも、右腕の貧弱なパフォーマンスを不運のせいだと考え、さらに数回試してみますか?
- あと何回試しますか?
この例は、バンディット問題における主要な関心事、「探索と活用のトレードオフ」を象徴しています。
より良いように見える選択肢を 探索 すべきか、それとも現在最良に見える選択肢を 活用 すべきか。探索と活用の間の正しいバランスを見つけることは、すべてのバンディット問題の中心にある根本的なジレンマです。

1.1 The Language of Bandits
バンディット問題は、学習者 と 環境 の間の逐次的なゲームです。ゲームは、$n$ラウンドにわたってプレイされます。ここで、$n$ は horizon (多分、「系列長」と訳す?)と呼ばれる正の整数です。各ラウンド $t \in [n]$ において、学習者はまず与えられた集合 $\mathcal{A}$ からアクション $A_t$ を選択し、その後環境が報酬 $X_t \in \mathbb{R}$ を明らかにします。
文献では、アクションはしばしば「腕」と呼ばれます。アクションの数が$k$である場合、k腕バンディット について話します。アクションの数が少なくとも2つあるが、実際の数が議論にとって重要でない場合は、多腕バンディット と書きます。多腕バンディットの中には、ペイオフが既知の決定論的な数である2つの現実的な腕を持つ 1本腕バンディット もあります。
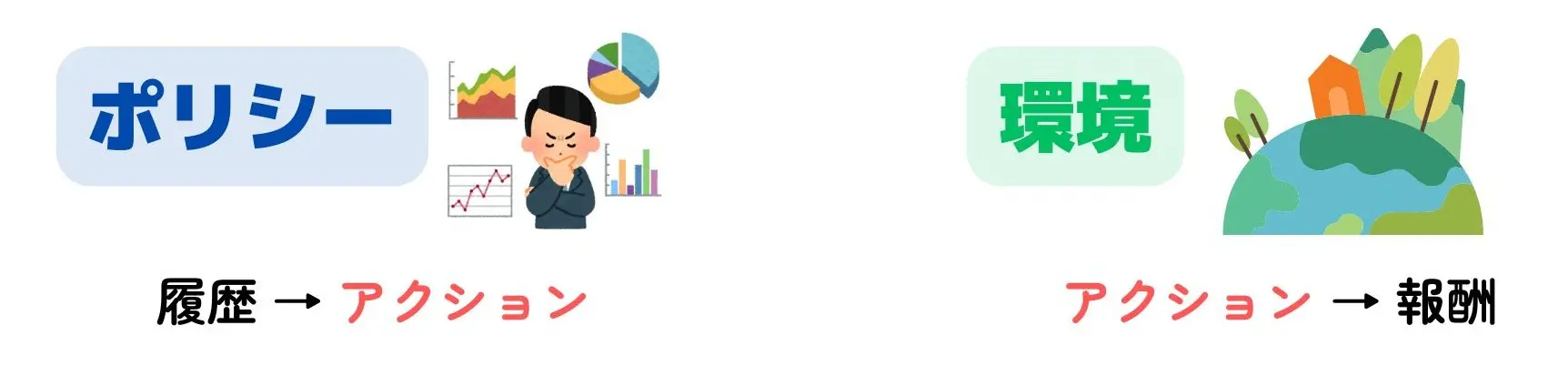
学習者は将来を見通すことはできず、その行動選択に使える情報は 過去 にのみ依存するべきです。つまり、$A_t$ は履歴 $H_{t-1} = (A_1, X_1, \dots, A_{t-1}, X_{t-1})$ にのみ依存すべきです。
学習者は環境と相互作用するために ポリシー(=方策) を採用します。ポリシー は、履歴 を アクション にマッピングするものです。環境 は、アクション を 報酬 にマッピングするものです。
学習者の最も一般的な目的は、$n$ラウンドにわたる総累積報酬 $\displaystyle\sum_{t=1}^n X_t$ を最大化することにつながるアクションを選択することです。
バンディット問題における根本的な課題は、環境が学習者にとって 未知 であることです。学習者が知っているのは、真の環境がある環境の集合 $\mathcal{E}$ 、すなわち 環境クラス に属しているということだけです。
この本のほとんどは、異なる環境クラスに対するポリシーの設計についてを扱います。場合によっては、フレームワークは、アクション や 報酬 だけでなく、副次的な観測 を含むように拡張されます。
次の問いは、「学習者(=アルゴリズム、ポリシー)を どのように評価するか 」です。
本書を通して、いくつかのパフォーマンス指標を議論しますが、私たちの努力のほとんどは リグレット を定義することに専念しています。詳細に踏み込むのを避けるため、ここにいくつかの非公式な定義を示します。
学習者のポリシー $\pi$ に対する リグレット は、$n$ ラウンドにわたってポリシー $\pi$ に従った場合の期待総報酬と、ポリシー $\Pi$ の集合における任意のポリシー $\pi' \in \Pi$ に対する期待総報酬の最大値との差
集合 $\Pi$ はしばしば 競合クラス と呼ばれます。
これは、リグレット は競合クラスにおける 最良のポリシー に対する学習者のパフォーマンスの 相対的な尺度 を測定するということです。
例を使って考えてみましょう。
アクション集合が $\mathcal{A} = \{1, 2, \dots, k\}$ であると仮定します。環境は 確率的ベルヌーイバンディット と呼ばれ、各ラウンド $t$ において、報酬 $X_t \in \{0, 1\}$ はバイナリ値(=2値)であり、アクション $a \in \mathcal{A}$ が与えられると、$X_t=1$ となる確率が $\mu_a$ であるようなベクトル $\mu \in [0, 1]^k$ が存在します。
このクラスの確率的ベルヌーイバンディットは、平均ベクトル によって特徴付けられます。
もし環境、つまりベクトル $\mu$ を知っていたなら、最適なポリシー は 最良のアクション $a^* = \text{argmax}_{a \in \mathcal{A}} \mu_a$ をプレイすることです。この意味で、この問題に対する自然な 競合クラス は、各ラウンドで常にアクション $i$ を選択する定常ポリシー $\Pi = \{\pi_1, \dots, \pi_k\}$ の集合です。$n$ ラウンドにわたるリグレットは、
であり、その期待値は環境と、使用されているポリシーにおけるランダム性に対して均すものです。最初の項は、最良の定常ポリシーによって期待される 最大報酬 であり、2番目の項は、学習者によって期待される報酬です。
固定されたポリシーと競合クラスに対して、リグレットは環境に依存します。
リグレットが大きくなる環境は、学習者が行動を誤るような環境です。もちろん、理想的なケースは、すべての環境に対してリグレットが小さくなるような場合です。
最悪ケースリグレット は、すべての可能な環境にわたる 最大リグレット です。バンディットの研究における中心的な問題の一つは、$n$ が増加するにつれてリグレットがどのように成長するかを理解することです。
ラウンド数 $n$ の増加でリグレットがどう変化するかを理解する。
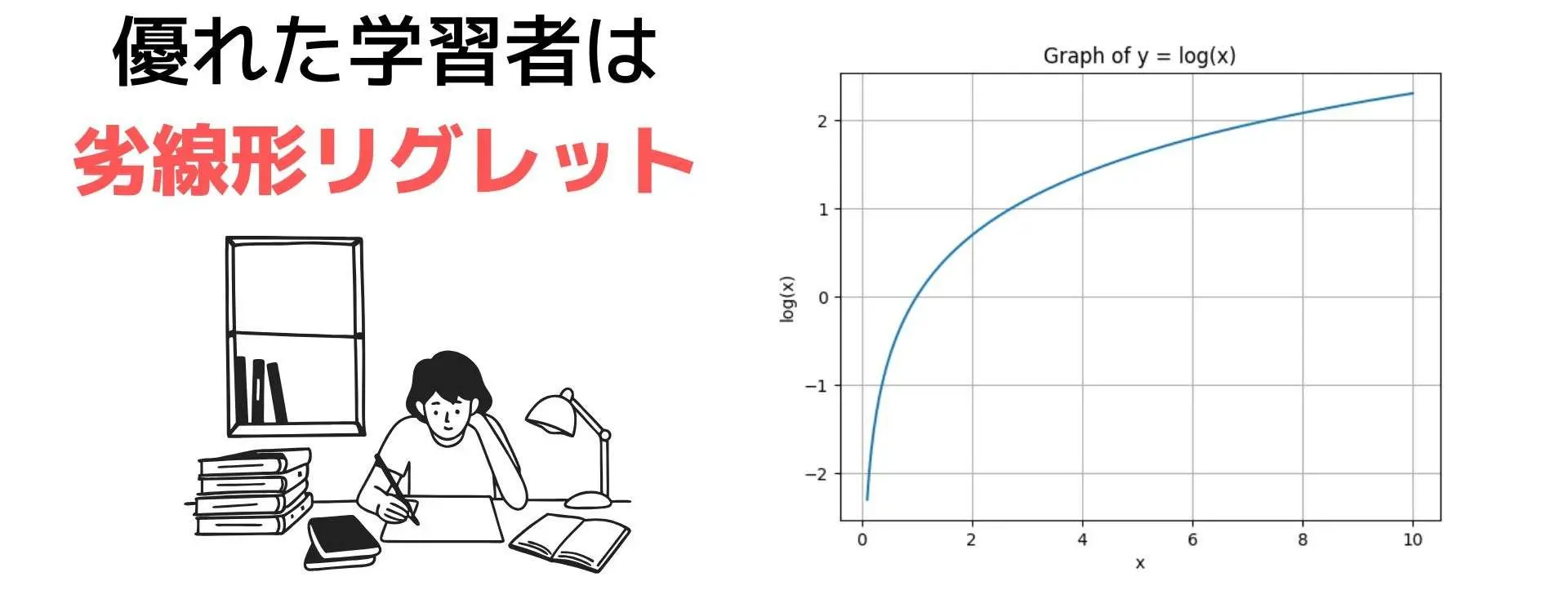
優れた学習者は、劣線形なリグレット を達成します。
これは、$R_n = o(n)$ すなわち、$n \to \infty$ で $\displaystyle \frac{R_n}{n} \to 0$ を意味します。
もちろん、以下のような疑問が浮かぶことでしょう。
- どのような状況下で劣線形リグレットは可能なのか?
- 主要な定数は何なのか?
例1.2 の 環境クラス では、$n$ に対して漸近的に $\Omega(\sqrt{n})$ であり、$R_n=O(\sqrt{n})$ であるポリシーが存在することが最終的に示されます。
大きな 環境クラス は、学習者 の知識が少ないことに対応します。また、より大きな 競合クラス は、より要求の厳しい基準に対応します。
時には、(a) リグレットに対する保証が意味を持つように、そして (b) 小さなリグレットを保証するポリシーが存在するように、両方のクラスを同時に制限する必要があります。
このフレームワークは、非常に豊かな環境クラスを使用してほとんど何でもモデル化できますが、あまりにも一般的すぎると、特定の種類の環境クラスと競合クラスに注意を限定することが不可能になる場合があります。このため、私たちは 確率的定常バンディット の研究に注意を限定します。
この場合、環境は、以前のアクションの選択と報酬に依存しない、特定の分布から各アクションに対する報酬を生成するように制限されています。
例1.2 の環境クラスはこの条件を満たしますが、多くの選択肢があります。
例えば、報酬は ベルヌーイ分布 ではなく ガウス分布 に従う可能性があります。この比較的小さな違いは、問題の性質を大きく変えることはありません。
より抜本的な変更は、アクション集合 $\mathcal{A}$ が $\mathbb{R}^d$ の部分集合であり、アクション $a \in \mathcal{A}$ を選択するための平均報酬が線形モデル $X_t = \langle a, \theta \rangle + \eta_t$ に従うと仮定することです。
ここで $\eta_t$ は標準ガウス分布(平均ゼロ、分散1)からサンプリングされる確率変数です。この場合、未知の量は $\theta\in\mathbb{R}^d$ であり、環境クラスはその可能な値 $\mathcal{E} = \{\theta \in \mathbb{R}^d\}$ に対応します。
いくつかの応用では、報酬が確率的かつ定常的であるという仮定はあまりにも制限的すぎるかもしれません。
世界はほとんど決定論的に見え、しばしば混沌とした様相を呈します。
もちろん、確率性はデータ内のパターンの説明に非常に成功してきましたが、このデータをモデリングの仮定として保つ必要があります。
しかし、確率的な仮定が成り立たない場合はどうなるでしょうか?
- 1ラウンドだけ、あるいはいくつかのラウンドで破られた場合は?
- 私たちのアルゴリズムは突然パフォーマンスが低下するのでしょうか?
- あるいは、アルゴリズムはモデリングの仮定に対する小さな逸脱やより大きな逸脱に対してロバストに開発されるのでしょうか?
極端なアイデアは、報酬がどのように生成されるかについてのすべての仮定を捨て、学習者の行動とは無関係に選択され、有界集合に属するという仮定だけをすることです。
これらの仮定だけが残る場合、私たちは敵対的バンディットと呼ばれる設定を得ます。

パチンコ屋さんで、悪意を持って店員にリアルタイムで操作されてる台みたいな
この設定で意味のあることを言うためのトリックは、競合クラスと一致することを期待するのではなく、最良の定常ポリシーよりもそれほど悪くないことを要求することです。このようにして、定常性の仮定は、環境を制約するのではなく、リグレットの定義に転送されます。
もちろん、これら2つの極端なケースの間はグラデーションです。
私たちは、報酬は確率的であるが、非定常である場合を考えます。あるいは、確率的バンディットに対するアルゴリズムのロバスト性を小さな敵対的な摂動に対して分析することもあります。
1.1.1 他の学習目標
リグレットはいくつかの方法で定義できることをすでに述べました。各々は、ポリシーの振る舞いのわずかに異なる側面を捉えています。リグレットは、環境に依存し、多目的な基準です。
私たちは、すべての可能な環境にわたってリグレットを小さく保ちたいと考えています。
単一の数値に変換する一つの方法は、平均を取ることです。これは、事前分布に関して累積リグレットを最小化することが目的であるベイズ的な視点に対応します。
報酬の合計を最大化することは、常に目的であるとは限りません。学習者は、$n$ ラウンド後に準最適なポリシーを見つけたいだけで、それらのラウンドで蓄積された実際の報酬は重要でない場合があります。
1.1.2 バンディットフレームワークの限界
本書で研究されているバンディット問題の際立った特徴の1つは、学習者が将来の計画を立てる必要がないことです。
より正確には、学習者の利用可能な選択肢と将来の報酬は、今日の決定によって影響を受けません。長期的な計画を必要とする問題は、本書の範囲外である 強化学習 の領域に分類されます。
バンディットフレームワークのもう1つの限界的な仮定は、学習者が各ラウンドで報酬を観察することです。これは 部分的なモニタリング と呼ばれ、第37章のトピックです。しばしば、環境自体が戦略的なエージェントで構成されており、学習者はその決定を考慮に入れる必要があります。
この問題はゲーム理論で研究されており、それ自体が1冊の本を必要とするでしょう。
1.2 応用
A/Bテスト
会社のデザイナーは、「今すぐ購入」ボタンを製品ページの上部に配置するか、下部に配置するかを決定しようとしています。古い時代では、彼らはユーザーを2つのグループに分け、10,000人の試行にコミットしていました。
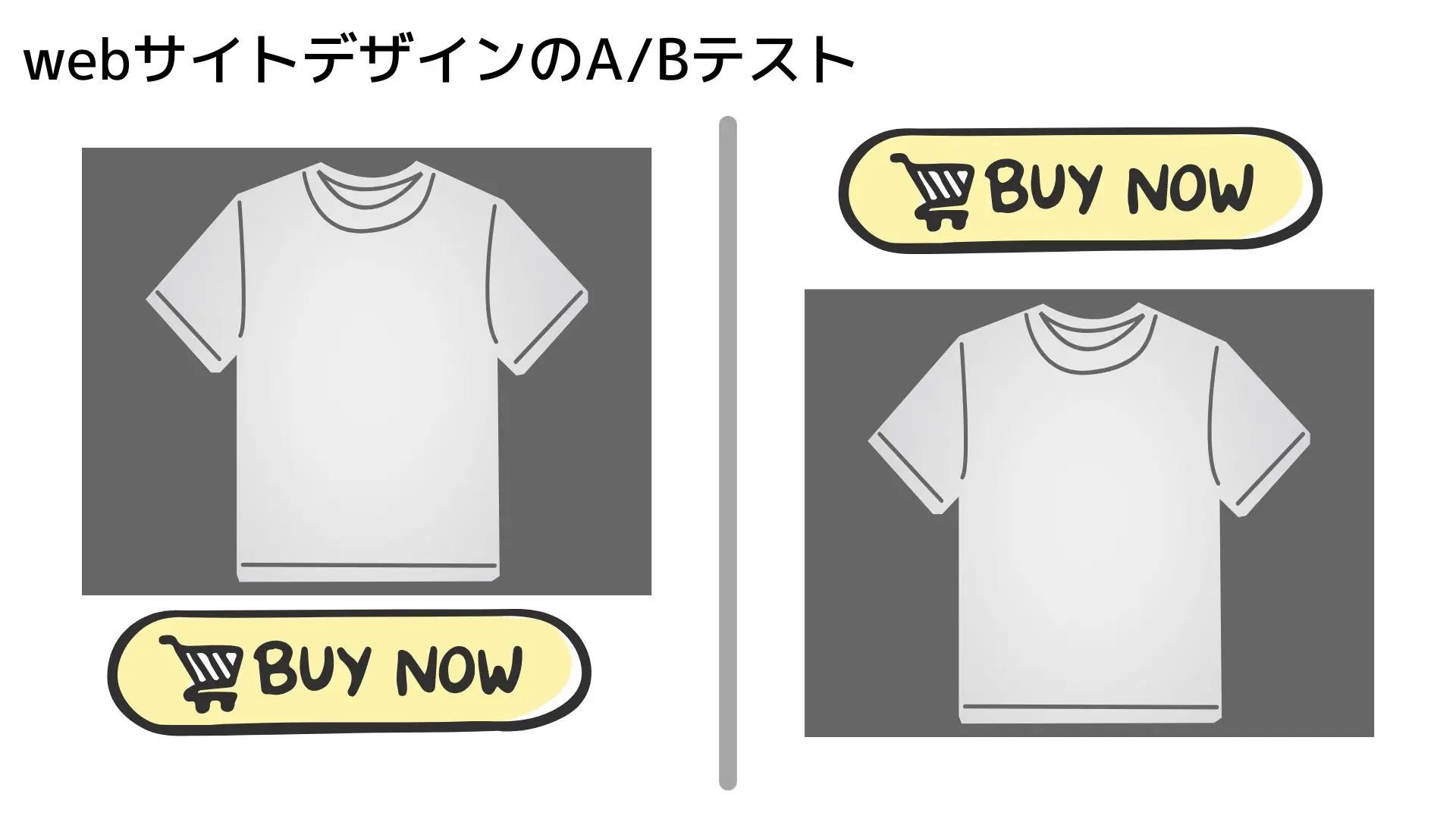
各グループにはサイトの異なるバージョンが表示され、統計家がデータを調べて、どちらのバージョンが優れているかを決定します。このアプローチの問題点は、テストの 非適応性 です。例えば、効果量が大きい場合、テストは早期に中止される可能性があります。
この問題をバンディットに適用する1つの方法は、ユーザーがサイトへのリクエストを行う各時間 $t$ で、バンディットアルゴリズムがサイトの2つのバージョンのうちどちらを表示するかを選択し、報酬はユーザーが製品を購入した場合は$X_t = 1$、そうでない場合は $X_t=0$ となります。アルゴリズムは、アクション $A_t \in \{\text{siteA}, \text{siteB}\}$ を選択します。
従来のA/Bテストでは、統計家の目的はどちらのウェブサイトが優れているかを判断することです。バンディットアルゴリズムを使用する場合、試行を終了する必要はありません。
アルゴリズムは、どちらかのバージョンを他方よりも頻繁に表示すべきかを自動的に決定します。たとえ本当の目的がどちらのサイトが最適かを特定することであっても、A/Bプロセスに早期停止や適応的なサンプリングを追加することは、バンディット理論からの技術を使用して行うことができます。これはこの本の焦点ではありませんが、いくつかの基本的な考え方は第35章で説明されています。
A/B テストというと Web での話だと思われがちだが、実店舗で行った例もある。「chocoZAP」だ。覆面店舗を47店舗展開し、どのようなサービスが刺さるのかを実店舗で A/B テストし、そこでの知見を活かした結果、急速に広がった。
47店舗でA/Bテストをくり返した結果、いろいろなことが見えてきました。たとえば、さまざまな部位を鍛えられるマルチマシンよりも、一部位だけを鍛えるシンプルなマシンのほうが好評だったり、対面や遠隔でトレーナーが教えるスタジオプログラムがあまり好まれなかったり。そうした反応を踏まえて『美容サービスも取り入れた設備』『完全無人で24時間運営』『月額2,980円』のビジネスモデルでスタートすることにしました(鈴木氏)
広告配置
広告配置では、各ラウンドはウェブサイトを訪れるユーザーに対応し、アクションの集合 $\mathcal{A}$ は利用可能なすべての広告の集合です。これは標準的な多腕バンディット問題として扱うことができ、各ラウンドでポリシーは広告 $A_t \in \mathcal{A}$ を選択し、報酬はユーザーが広告をクリックした場合は $X_t=1$、そうでない場合は $X_t=0$ となります。

Amazonのような企業では、広告はよりターゲットを絞るべきです。最近ロッククライミングシューズを購入したユーザーは、ハーネスを購入する可能性が他のユーザーよりもはるかに高いはずです。
この追加情報を取り入れる標準的な方法は、ユーザーに関する情報(コンテキスト)を使用することです。最も単純な形式では、ユーザーをクラスタリングし、各クラスターに対して別々のバンディットアルゴリズムを実装することを意味するかもしれません。この本の多くは、学習者のパフォーマンスを向上させるためにサイド情報をどのように使用するかという問題に専念しています。
これは、現実世界が厄介であることを強調する良い場所です。利用可能な広告のセットは、ラウンドごとに変化する可能性があります。ユーザーからのフィードバックは、多くのラウンドにわたって遅延する可能性があります。
最後に、真の目的は単にクリックを最大化することではないかもしれません。ユーザー満足度、多様性、鮮度、公正さなど、いくつかの指標も重要です。これらは、現実世界でバンディットアルゴリズムを実装する際に生じる問題の種類です。この本はこれらの問題をすべて取り上げるわけではありません。代わりに、どのような課題が生じても、それに対応する独創的な解決策を考案できるような基礎と深い理解を提供することに焦点を当てています。
推薦サービス
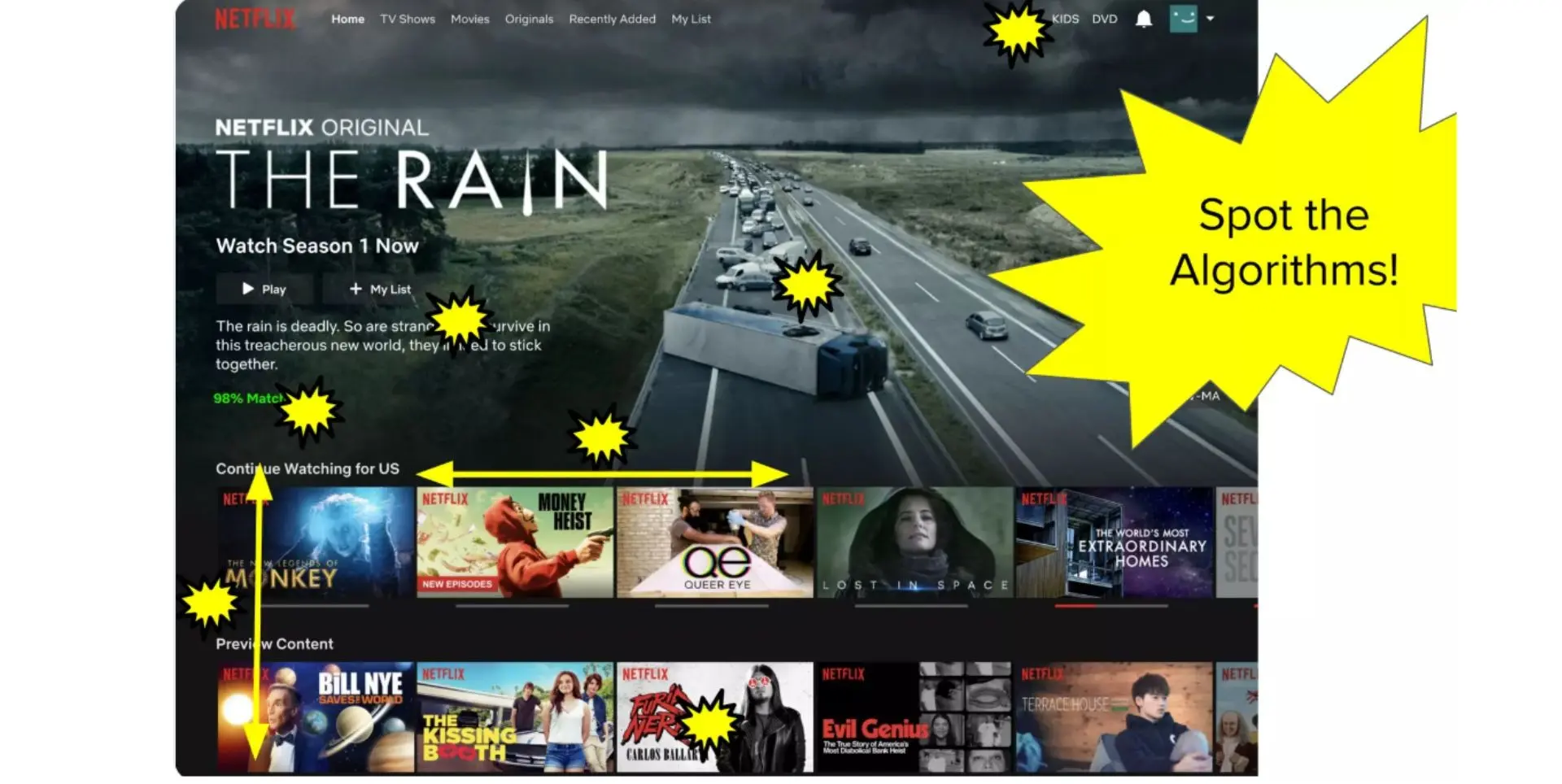
Netflixは、「あなたの閲覧リスト」でどの映画を最も目立つように配置するかを決定しなければなりません。
広告配置と同様に、ユーザーはページに順番に到着し、報酬は
(a) あなたが映画を観たかどうか
(b) あなたがそれを肯定的に評価したかどうか
で測定できます。
「あなたにおすすめ」機能には、多くの課題があります。
まず、Netflixは映画のリストを表示し、可能なアクションのセットは組み合わせ的に大きくなります。第二に、各ユーザーは比較的少数の映画しか見ず、個々のユーザーは異なります。
これは「協調フィルタリング」として知られるアプローチを示唆しています。低ランク行列分解は協調フィルタリングで人気のあるアプローチです。
第三に、これはオフラインの問題ではありません。学習アルゴリズムは、ユーザーが何を見るかを選択し、これがデータに影響を与えます。ユーザーに AlphaGo の映画が推奨されなければ、それを見る人はほとんどおらず、この映画に関するデータの量は乏しくなります。
➡ 関連:反実仮想機械学習、Offline Evaluation
ネットワークルーティング
興味深い構造を持つ別の問題は、ネットワークルーティング です。
学習者は、ネットワーク上の最短経路 を通してインターネットトラフィックを誘導しようとします。各ラウンドで、学習者はデータパケットの始点/終点の宛先を受け取ります。アクションのセットは、既知のグラフ上の適切な始点と終点を持つすべてのパスのセットです。
この場合のフィードバックは、パケットが受信者に届くのにかかる時間であり、報酬はその時間の負の値です。ここでも、アクションセットは 組み合わせ的に大きい です。比較的少数のグラフは膨大な数のパスを持つことができます。ルーティング問題は、業務研究で使用される輸送システムなどのより物理的なネットワークに明らかに適用できます。
動的価格設定
動的価格設定では、企業は製品の価格を自動的に最適化しようとします。ユーザーは順番に到着し、学習者が価格を設定します。ユーザーは、価格が自分の評価額よりも低い場合にのみ製品を購入します。
この問題を面白くするのは、
(a)学習者は製品の評価額を実際には観察せず、価格が低すぎたか高すぎたかというバイナリ信号だけを観察すること
(b)価格設定には単調性構造があること
です。
ユーザーがある価格、10ドルで購入した場合、彼らは間違いなく5ドルで購入したでしょうが、11ドルで購入したかどうかはわかりません。また、可能なアクションのセットは連続的です。
待機問題
毎日、あなたはバスか徒歩で通勤することを選びます。バスに乗れば、移動時間はわずか5分ですが、時刻表は信頼できず、バスの到着時間は不明で確率的です。一方、歩くと、バス停からかなり離れた美しい川沿いを30分かかります。
学習者は、職場に着くまでの時間を最小限に抑えるための方針を考案しようとします。あまりにも長く待ちすぎると、バス停で時間を無駄にし、情報を得ます。しかし、歩くことで時間の損失を抑え、情報を得ることもできます。
バスを待つことは私たち全員が直面する問題ですが、この設定には他にも応用があります。
たとえば、非アクティブになった後にハードドライブをスリープモードにするか、交通信号機をオフにするかを決定することです。待機問題の統計的な部分は、バスが到着する前に歩くことを選択した日にデータが打ち切られることです。このデータの分布は、生存分析のサブフィールドで分析される問題です。
リソース配分
オペレーションズリサーチの大きな部分は、希少なリソースを割り当てるための戦略を設計することに焦観点を当てています。需要や供給のダイナミクスが不確かな場合、リソースの割り当てはバンディット問題の要素を帯びています。需要について部分的な情報しか明らかにしないリソースをあまりにも少なく割り当てることは無駄ですが、あまりにも多くのリソースを割り当てることもまた無駄です。もちろん、リソース配分は広範であり、多くの問題は、長期的な計画の必要性のように、バンディット問題に典型的ではない構造を示します。
木探索
UCTアルゴリズム は、完全情報ゲームプレイで一般的に使用される 木探索アルゴリズム です。その名前は、アルゴリズムが各反復で木を逐次的に構築するという考えに由来します。
アルゴリズムは3つのステップを踏みます。
(1) 根から葉まで経路を選択し、
(2) (可能であれば) 葉を展開し、
(3) 葉からゲームの終わりまでモンテカルロロールアウトを実行します。
バンディットアルゴリズムの貢献は、葉への経路を選択することにあります。木の中の各ノードで、これまでに観測された報酬の系列に基づいて子を選択するためにバンディットアルゴリズムが使用されます。
結果として得られるアルゴリズムは、これまでのところ分析的にほとんど理解されていませんが、より重要なことに、ゲームプレイの問題で優れた経験的パフォーマンスを示しています。
