漸化式を解くためのマスター法

アルゴリズムの実行時間解析、特に分割統治法に基づくアルゴリズムでは、その計算量を表す漸化式を解くことが求められる。マスター法は、特定の形式の漸化式に対して、その解を体系的に導出するための手法である。

マスター法の原理と適用方法について、具体例を交えながら解説する。

マスター法の概要

$$T(n) = aT(n/b) + f(n)$$

という形式の漸化式の解を、3つのケースに分類して求めるための定理に基づく手法である。多くの分割統治アルゴリズムの実行時間解析に応用できる。

マスター法の対象となる漸化式

マスター法が適用可能な漸化式の形式は以下の通りである。

マスター漸化式の定義

$$T(n) = aT(n/b) + f(n)$$

ここで、

  • $a \ge 1$: サイズ $n/b$ の部分問題の数
  • $b \gt 1$: 各部分問題のサイズの、元の問題のサイズに対する割合の逆数
  • $f(n)$: 問題を部分問題に分割するコストと、部分問題の解を統合するコストの合計（駆動関数）

この形式の漸化式をマスター漸化式と呼ぶ。

細かい話をすると、 $n/b$ が整数にならない場合は床関数 $\lfloor n/b \rfloor$ や天井関数 $\lceil n/b \rceil$ を用いるのだが、マスター法による漸近的な解では結局どっちにしても $\Theta(n\lg n)$ なので、特にこだわらずに簡略化して $n/b$ と記述することにする。

マスター定理

マスター法の理論的土台は、マスター定理によって与えられる。

Tip

マスター定理の核心は、分水界関数 (water-shed function) $n^{\log_b a}$ と駆動関数 (driving function) $f(n)$ の漸近的な増加率の比較にある。

定理 4.1 (マスター定理) $a \ge 1$ および $b > 1$ を定数とし、$f(n)$ を十分大きいすべての実数上で定義されている非負の駆動関数とする。$n\in\mathbb{N}$ 上の漸化式 $T(n) = aT(n/b) + f(n)$ の漸近的な挙動は、以下の3つのケースによって特徴づけられる。（ここで、$aT(n/b)$ は実際 $a'\geq 0, \; a''\geq 0, \; a=a'+a''$ なる定数に対して $a'T(\lfloor n/b \rfloor) + a''T(\lceil n/b \rceil)$ を意味するものとして解釈する）：

  1. ある定数 $\epsilon > 0$ があって $f(n) = O(n^{\log_b a - \epsilon})$ ならば、$T(n) = \Theta(n^{\log_b a})$ である。
  2. ある定数 $k \ge 0$ があって $f(n) = \Theta(n^{\log_b a} \lg^k n)$ ならば、$T(n) = \Theta(n^{\log_b a} \lg^{k+1} n)$ である。
  3. ある定数 $\epsilon > 0$ があって $f(n) = \Omega(n^{\log_b a + \epsilon})$ であり、かつ、ある定数 $c < 1$ と十分大きな全ての $n$ に対して $a f(n/b) \le c f(n)$ (これを正則条件という) を満たすならば、$T(n) = \Theta(f(n))$ である。

以下では、各ケースについて詳細を見ていく。

1️⃣ ケース1: $f(n)$ が $n^{\log_b a}$ に対して多項式的に小さい場合

Case1

ケース1 条件: ある定数 $\epsilon > 0$ があって、$f(n) = O(n^{\log_b a - \epsilon})$

ケース1 結論: $T(n) = \Theta(n^{\log_b a})$

解釈: 再帰呼び出しによって生成される部分問題の総コスト（再帰ツリーの葉におけるコストの総和）が、全体の計算量を支配する。

これはつまり、分水界関数 $n^{\log_{b}a}$ が駆動関数 $f(n)$ より多項式的に速く増加しなければならないことを要請している。

言い換えると、$n^{\log_{b}a}$ はある定数 $\epsilon >0$ に対して漸近的に少なくとも $f(n)$ の $\Theta(n^{\epsilon})$ 倍になっている必要がある、ということだ。

このケースは、再帰ツリーの葉の処理コストが、それ以外のレベルでの処理コスト（分割・統合コスト）の総和よりも漸近的に大きい状況に対応する。

Example

例: $T(n) = 9T(n/3) + n$

  1. $a=9, b=3, f(n)=n$
  2. 分水界関数: $n^{\log_b a} = n^{\log_3 9} = n^2$
  3. 比較: $f(n)=n$ と $n^{\log_b a} =n^2$ なので、たとえば $\epsilon=1$ とすれば $n = O(n^1)$ であり、条件$n = O(n^{2-\epsilon})$ を満たす $\epsilon > 0$ が存在することが分かった。
  4. 結果: ケース1を適用して、$T(n) = \Theta(n^2)$ とわかる。

2️⃣ ケース2: $f(n)$ と $n^{\log_b a}$ がほぼ同程度の増加率である場合

Case2

ケース2 条件: ある定数 $k \ge 0$ があって、$f(n) = \Theta(n^{\log_b a} \lg^k n)$

ケース2 結論: $T(n) = \Theta(n^{\log_b a} \lg^{k+1} n)$

解釈: 再帰ツリーの各レベルにおけるコストがほぼ等しく、全体のコストは「レベル数 $\times$ 各レベルのコスト」に比例する。

駆動関数 $f(n)$ と分水界関数 $n^{\log_b a}$ が、高々対数因子 $\lg^k n$ の違いで漸近的に等しい場合である。このとき、解には対数因子が一つ加わる。

Example

例: マージソートの漸化式 $T(n) = 2T(n/2) + \Theta(n)$

  1. $a=2, b=2, f(n)=\Theta(n)$
  2. 分水界関数: $n^{\log_b a} = n^{\log_2 2} = n^1 = n$
  3. 比較: $f(n)=\Theta(n)$ と $n^{\log_b a} =n$ なのでたとえば $k=0$ とすれば $f(n) = \Theta(n \lg^0 n)$ となり、条件を満たす $k\ge 0$ が存在することが分かった。
  4. 結果: ケース2を適用して、$T(n) = \Theta(n \lg^{0+1} n) = \Theta(n \lg n)$ とわかる。
Note

ケース2で特によくあるのは $k=0$ の場合、すなわち $f(n) = \Theta(n^{\log_b a})$ であり、このとき $T(n) = \Theta(n^{\log_b a} \lg n)$ となる。

3️⃣ ケース3: $f(n)$ が $n^{\log_b a}$ に対して多項式的に大きく、かつ正則条件を満たす場合

Case3

ケース3 条件1: ある定数 $\epsilon > 0$ があって $f(n) = \Omega(n^{\log_b a + \epsilon})$ ケース3 条件2 (正則条件): ある定数 $c < 1$ と十分大きな $n$ に対して $a f(n/b) \le c f(n)$

ケース3 結論: $T(n) = \Theta(f(n))$

解釈: 再帰の最初のステップ（ルートノード）における分割・統合コスト $f(n)$ が、全体の計算量を支配する。

Warning

正則条件の確認

ケース3の適用には、$f(n)$ が $n^{\log_b a}$ よりも多項式的に大きいことに加え、正則条件 $\exists c < 1, \; a f(n/b) \le c f(n)$ を満たす必要がある。この条件は、$f(n)$ の増加が局所的なものではなく、再帰プロセス全体を通じてそのコストが支配的であり続けることを保証するものといえる。

Example

例: $T(n) = 3T(n/4) + n \lg n$

  1. $a=3, b=4, f(n)=n \lg n$
  2. 分水界関数: $n^{\log_b a} = n^{\log_4 3} \approx n^{0.79248}$
  3. 比較: $f(n)=n \lg n$ と $n^{0.79248}$ なので、たとえば $\epsilon=0.1$ とすれば $n \lg n = \Omega(n^{0.893})$ であり、 $n \lg n = \Omega(n^{0.793+\epsilon})$ なので、条件1は満たされる。
  4. 正則条件: $3 \cdot \left(\frac{4}{n}\right) \lg\left(\frac{4}{n}\right) \le c \cdot n \lg n$ $\left(\frac{4}{3}\right)\; n \;\left(\lg n - \lg 4\right) \le c n \lg n$ 十分大きな $n$ に対して $\lg n - \lg 4 \approx \lg n$ と近似できるため、$c=3/4$ 付近でこの不等式は成立する。もう少しちゃんと言うと、$c$ として $3/4$ よりわずかに大きい値（たとえば、$c=0.8$ とか）を選べば、十分大きな $n$ に対して成立する。よって、条件2は満たされる。
  5. 結果: ケース3を適用して、$T(n) = \Theta(n \lg n)$
  1. 比較の補足： $\frac{f(n)}{n^{(\log_{b}​a)+\epsilon}}​\approx\frac{n\log n}{n^{0.79248+\epsilon}}​=n^{1−0.79248-\epsilon}\log n = n^{0.20752-\epsilon}\log n$

なので、$\epsilon$ は $0<\epsilon<0.20752$ でとれば、この比は発散する。

マスター法の適用手順

マスター法を用いて漸化式を解く手順は以下の通りである。

Todo

マスター法適用手順

  1. 漸化式 $T(n) = aT(n/b) + f(n)$ から、定数 $a, b$ および関数 $f(n)$ を特定する。
  2. 分水界関数 $n^{\log_b a}$ を計算する。
  3. 駆動関数 $f(n)$ と分水界関数 $n^{\log_b a}$ の漸近的な増加率を比較する。
    • ケース1に該当するか: $f(n)$ が $n^{\log_b a}$ に対して多項式的に小さいか？
    • ケース2に該当するか: $f(n)$ が $n^{\log_b a}$ と（対数因子を除いて）ほぼ同じ増加率か？
    • ケース3に該当するか: $f(n)$ が $n^{\log_b a}$ に対して多項式的に大きく、かつ正則条件を満たすか？
  4. 該当するケースの結論を適用し、$T(n)$ の漸近的評価を得る。
  5. 上記のいずれのケースにも当てはまらない場合、マスター法は適用できない。

マスター法が適用できない場合

マスター法は強力な手法であるが、全てのマスター漸化式を解けるわけではない。これまでにやった3つのケースに当てはまらない漸化式はマスター法では解けない。

Warning

マスター法の適用限界

  • ケース1とケース2の間のギャップ: $f(n)$ が $n^{\log_b a}$ よりも漸近的に小さいが、多項式的には小さくない場合は適用できない。たとえば $T(n)=2T(n/2) + n/\lg n$ だと、駆動関数 $f(n) = n^{\log_b a} / \lg n$ で分水界関数 $n$ よりも漸近的に対数的な増加をする。
  • ケース2とケース3の間のギャップ: $f(n)$ が $n^{\log_b a}$ よりも漸近的に大きいが、多項式的には大きくない場合は適用できない。
  • ケース3の正則条件不成立: $f(n)$ が $n^{\log_b a}$ よりも多項式的に大きいものの、正則条件を満たさない場合。
Failure

適用できない漸化式の例: $T(n) = 2T(n/2) + n/\lg n$

  • $a=2, b=2 \implies n^{\log_b a} = n$.
  • $f(n) = n/\lg n$.
  • $f(n)$ は $n$ より小さいが、$O(n^{1-\epsilon})$ の形ではない。
  • $f(n)$ は $\Theta(n \lg^k n)$ ($k \ge 0$) の形ではない ($k=-1$ は定義外)
  • $f(n)$ は $n$ より大きくない。

この漸化式はマスター法のどのケースにも該当しない。このような場合、代入法、再帰ツリー法、あるいはAkra-Bazziの定理といった他の手法を検討する必要がある。ちなみに、この漸化式の解は $T(n) = \Theta(n \lg \lg n)$ である。

マスター法適用例

練習問題 4.5-1 から抜粋して、マスター法の適用例をいくつか示す。

Example

a. $T(n) = 2T(n/4) + 1$

  • $a=2, b=4, f(n)=1$. 分水界関数は $n^{\log_4 2} = n^{1/2} = \sqrt{n}$.
  • $f(n)=1 = O(n^{1/2-\epsilon})$ たとえば $\epsilon=1/2$ のとき $1 = O(n^0) = O(1)$
  • 結論 (ケース1): $T(n) = \Theta(\sqrt{n})$.
Example

b. $T(n) = 2T(n/4) + \sqrt{n}$

  • $a=2, b=4, f(n)=\sqrt{n}$. 分水界関数は $n^{\log_4 2} = \sqrt{n}$.
  • $f(n)=\sqrt{n} = \Theta(\sqrt{n} \lg^0 n)$ ($k=0$).
  • 結論 (ケース2): $T(n) = \Theta(\sqrt{n} \lg n)$.
Example

d. $T(n) = 2T(n/4) + n$

  • $a=2, b=4, f(n)=n$. 分水界関数は $n^{\log_4 2} = \sqrt{n}$.
  • $f(n)=n = \Omega(n^{1/2+\epsilon})$ たとえば $\epsilon=1/2$ のとき $n = \Omega(n^1)$
  • 正則条件: $a f(n/b) = 2 \cdot (n/4) = n/2$. $cf(n) = cn$. $n/2 \le cn$ は $1/2 \le c$ を意味する。$c=3/4 (<1)$ などで成立。
  • 結論 (ケース3): $T(n) = \Theta(n)$.

ここまでのまとめ

Summary

マスター法の要点

  • $T(n) = aT(n/b) + f(n)$ の形式の漸化式に適用される。
  • $n^{\log_b a}$ と $f(n)$ の漸近的な比較に基づき、3つのケースに分類される。
    1. $f(n)$ が $n^{\log_b a}$ に対して多項式的に小さい場合、$T(n) = \Theta(n^{\log_b a})$。
    2. $f(n)$ が $n^{\log_b a}$ と（対数因子を除き）同程度の増加率の場合、$T(n) = \Theta(n^{\log_b a} \lg^{k+1} n)$。
    3. $f(n)$ が $n^{\log_b a}$ に対して多項式的に大きく、かつ正則条件を満たす場合、$T(n) = \Theta(f(n))$。
  • 適用できない「ギャップ」が存在することに留意が必要である。

マスター法は、条件に合致する漸化式に対して、その解を効率的に導出するための有用なツールである。ただし、その適用範囲と限界を正しく理解することが重要である。適用できない場合には、他の解析手法を検討する必要がある。

練習問題

練習問題4.5-2

徳川教授は Strassenのアルゴリズムよりも漸近的に高速な行列乗算アルゴリズムを設計したいと考えている。彼のアルゴリズムは分割統治法に基づいており、各行列を $n/4 \times n /4$ 型に分割し、分割段階と結合段階に $\Theta(n^2)$ 時間かかる。Strassenのアルゴリズムを凌ぐために自身のアルゴリズムが生成しなければならない部分問題数を決定する必要がある。アルゴリズムが $a$ 個の部分問題を生成すると仮定すると、実行時間 $T(n)$ を特徴づける漸化式は $T(n)=aT(n/4)+\Theta(n^2)$ である。徳川教授のアルゴリズムが Strassenのアルゴリズムよりも漸近的に高速であるような最大の整数 $a$ の値を求めよ。

Strassen 法の計算量は

$$ T_{\text{Strassen}}(n)=\Theta\!\bigl(n^{\log_2 7}\bigr) =\Theta\!\bigl(n^{\,2.8074\ldots}\bigr) $$

「徳川教授のアルゴリズム」の漸化式は、以下の通り：

$$ T(n)=a\,T\bigl(n/4\bigr)+\Theta(n^2) $$
$$ T(n)=a\,T(n/4)+f(n) $$

の漸近的振る舞いは：

  • $a < 16$ のとき：ケース3 $\implies T(n) = \Theta(n^2)$
  • $a = 16$ のとき：ケース2 $\implies T(n) = \Theta(n^2 \log n)$
  • $a > 16$ のとき：ケース1 $\implies T(n) = \Theta(n^{\log_4 a})$

となる。以下はその詳しい説明：

  1. $$f(n)=O\bigl(n^{\log_{4}a-\epsilon}\bigr)$$
    $$T(n)=\Theta\!\bigl(n^{\log_{4}a}\bigr)$$

    となる。これは、$\log_4 a>2$ つまり $a>16$ かつ $\log_4 a-2\ge\epsilon>0$ のときである。

  2. $$f(n)=\Theta\bigl(n^{\log_{4}a}\,\lg^k n\bigr)$$
    $$T(n)=\Theta\bigl(n^{\log_{4}a}\,\lg^{\,k+1}n\bigr)$$

    となる。これは、 $\log_4 a=2$ つまり $a=16$ かつ $f(n)=\Theta(n^2)$ のとき（ $k=0$ ) である。

  3. $$f(n)=\Omega\bigl(n^{\log_{4}a+\epsilon}\bigr)\quad\text{かつ}\quad　a\,f(n/4)\le c\,f(n)\quad(\exists\,c<1)$$
    $$T(n)=\Theta\bigl(f(n)\bigr)=\Theta(n^2)$$

    となる。これは、 $\log_4 a<2$ つまり $a<16$ かつ正則条件 $a\,(n/4)^2\le c\,n^2$ つまり $a/16<1$ が成り立つときである。

Strassen 法 $\Theta(n^{\log_2 7})\approx\Theta(n^{2.8074})$ より速い条件

教授のアルゴリズムが Strassen より漸近的に高速なのは、

$$ \max\!\bigl(2,\;\log_4 a\bigr) \;<\;\log_2 7\approx2.8074 $$
  • $a<16$ のとき：指数は $2$ → $2<2.8074$ で OK
  • $a=16$ のとき：指数は $2$（ログ因子付きでも実質べきは 2）→ OK
  • $a>16$ のとき：指数は $\log_4 a<\log_2 7$ である必要があり
$$ \log_4 a<\log_2 7 \;\Longleftrightarrow\; a<4^{\log_2 7}=49 $$

したがって「Strassen より速い」ための整数 $a$ の範囲は

$$ 1\le a\le48 $$
$$ a = 48 $$

余談

Wiki によるとさらにオーダーを小さくしたアルゴリズムもあるみたいですね。

Quote

As of April 2024, the best announced bound on the asymptotic complexity of a matrix multiplication algorithm is $O(n^{2.371552})$ time, given by Williams, Xu, Xu, and Zhou. This improves on the bound of $O(n^{2.3728596})$ time, given by Alman and Williams. However, this algorithm is a galactic algorithm because of the large constants and cannot be realized practically.

2024年4月時点で、行列積アルゴリズムの漸近的計算量に関して発表されている最良の上界は、Williams氏、Xu氏、Xu氏、Zhou氏による $O(n^{2.371552})$ です。これは、Alman氏とWilliams氏による従来の記録である $O(n^{2.3728596})$ を更新するものです。しかしながら、このアルゴリズムは定数項が非常に大きいため銀河系アルゴリズム（実用的ではない理論上のアルゴリズム）であり、実用化は不可能です。

Matrix multiplication algorithm - Wikipedia

Williams さんの論文はコレ↓↓ https://arxiv.org/abs/2307.07970

実用上の話でいうと、Numpyって行列乗算の中身の実装どうなってるんだ？っていうのが気になったので軽く調べると、

  • numpy.matmal ( @ 演算子と同じ) は strassen 法を採用していない
    • It uses an optimized BLAS library when possible (see numpy.linalg).
      • numpy.matmul — NumPy v2.2 Manual
        • BLASとは、Basic Linear Algebra Subprogramsの略です。難しく言うと、基本的な線形演算のライブラリ、簡単にいえば、行列やベクトルの基本的な計算をやってくれる関数群です。LAPACKなど他の数値計算を行うライブラリなどで必要となるなど、数値計算には欠かせないライブラリ群です。数値計算を行うソフトウェアのインストールにこれをインストールすることが求められることもありますし、MATLABなどにもこれらのルーチンが乗っかって居るようです。CPUの適正を考えて実装されていますので、非常に高速に動作します。
        • BLASの簡単な使い方
        • BLAS = すごい最適化された線形演算のライブラリ
    • という感じで BLAS のライブラリが使えるならそれを使っており、そうでない場合は C で実装された $O(n^3)$ のループで計算してる
    • ここみればどういう実装か見れる
    • https://github.com/numpy/numpy/blob/v2.1.0/numpy/_core/src/umath/matmul.c.src

BLAS のライブラリが使えない部分の行列乗算の実装部分はこの辺？↓↓↓

https://github.com/numpy/numpy/blob/v2.1.0/numpy/_core/src/umath/matmul.c.src を見ると以下のような対応になってるっぽい。

dtype BLAS のライブラリが扱えるか NumPy の対応
float32/float64・complex64/complex128 Yes cblas_sgemm/dgemm/zgemm などに投げる
bool_ No C言語BOOL_matmul_inner_noblas
object_ No C言語OBJECT_matmul_inner_noblas

じゃあ、OpenBLASとかのBLASのライブラリがどうやって計算してるか？？を調べようと思ったんですけど、カーネルの最適化がどうこうとか出てきて難しくてよくわかんなかったです。

連続マスター定理の証明

ここまでマスター法という強力なツールを使って、特定の形の漸化式を解く方法を見た。しかし、「なぜそうなるのか？🤔」という数学的な背景については触れていない。ここではめんどくさいが数学科的には大事な部分について確認していく。

この節では、マスター定理の証明そのものではなく、その変種である「連続マスター定理 (continuous master 定理)」の証明を通じて、マスター定理が成り立つ仕組みの主要なアイデアを探求する。なぜそうするかというと、連続マスター定理は、入力 $n$ を（床関数や天井関数を気にしなくてよい）十分に大きな実数として扱うため、証明がいくぶん簡潔になるからだ。

Info

このセクションの目的

  • マスター定理の証明の核心的なアイデアを理解する。
  • 床関数や天井関数といった複雑さを排除した「連続」バージョンで考える。
  • 証明を追うことで、分割統治アルゴリズムの漸化式の挙動に対するより深い洞察を得る。

注意: マスター法を使うだけなら、この証明を理解する必要はない。しかし、アルゴリズムの数学的側面に興味がある方にとっては有益な内容となる。

証明は、2つの補題 (補題 4.2, 補題 4.3) と、それらを用いた連続マスター定理 (定理 4.4) の証明という構成になっている。

準備：再帰ツリーとコストの定式化 (補題 4.2)

まず、マスター漸化式 $T(n) = aT(n/b) + f(n)$ を再帰ツリーで展開したときの総コストを定式化する補題を見ていく。

補題 4.2

$a > 0, b > 1$ を定数とし、$f(n)$ を実数 $n \ge 1$ で定義された関数とする。漸化式

$$T(n) = \begin{cases} \Theta(1) & \text{if } 0 \le n < 1 \\ aT(n/b) + f(n) & \text{if } n \ge 1 \end{cases}$$

は、以下の解を持つ。

$$T(n) = \Theta(n^{\log_b a}) + \sum_{j=0}^{\lfloor \log_b n \rfloor} a^j f(n/b^j) \quad \quad (4.18)$$

証明：再帰ツリーによって解を定式化する

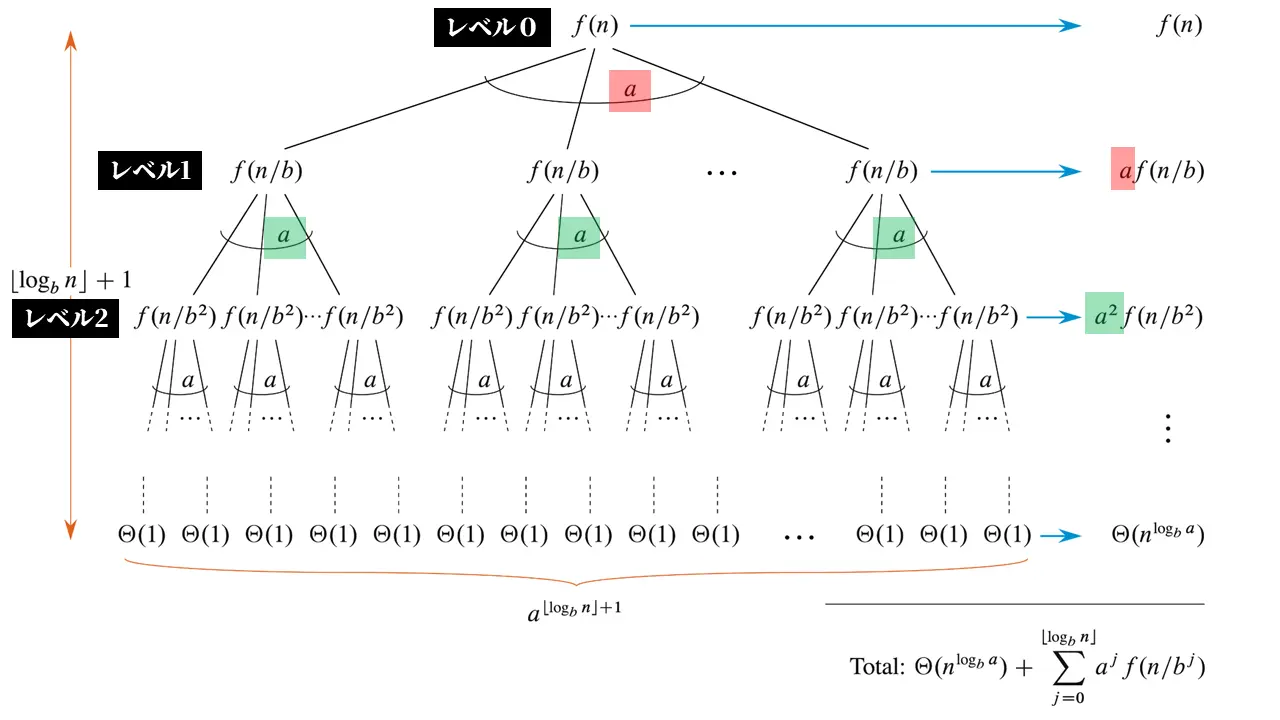教科書図4.3 に少し手を加えた。

(1) 再帰ツリーの構成

根（レベル 0）は問題サイズ $n$ を扱い、分割・統合に要するコストは $f(n)$ である。根からは $a$ 本の枝が伸び、各子ノードはサイズ $n/b$ の部分問題を引き受ける。同じ手順を繰り返すと、レベル $j$ には $a^{j}$ 個のノードが存在し、それぞれのコストが $f(n/b^{j})$ となる。

したがってそのレベルの合計コストは $a^{j}f(n/b^{j})$ である。

(2) ツリーの深さ

再帰は部分問題のサイズが 1 未満になるまで続く。条件 $n/b^{j}<1$ は $j>\log_b n$ と同値なので、展開が打ち切られる直前の内部レベルは $j_{\max}=\lfloor\log_b n\rfloor$ である。その次の深さ $j_{\max}+1$ が葉レベルに当たる。

(3) 葉の個数とその総コスト

葉の数は $a^{\,j_{\max}+1}=a^{\lfloor\log_b n\rfloor+1}$ である。指数法則 $a^{\log_b n}=n^{\log_b a}$ を使うと、この個数は $\Theta(n^{\log_b a})$ と評価できる。ベースケースのコストが定数 $\Theta(1)$ であるため、葉全体のコストは $\Theta(n^{\log_b a})$ になる。これは式 (4.18) に現れる第一項の由来である。

(4) 内部ノードの総コスト

深さ 0 から $j_{\max}$ までの各レベルのコストを足し合わせると

$$ \sum_{j=0}^{\lfloor\log_b n\rfloor} a^{\,j}\,f\!\left(\dfrac{n}{b^{j}}\right) $$

が得られる。これが式 (4.18) の第二項に当たる。

(5) 全体の和

葉にかかる $\Theta(n^{\log_b a})$ と、内部ノードにかかる総和とを足し合わせれば、(4.18) が成立し、補題 4.2 の主張が証明される。

（証明終わり）☑️

補題が示すもの

式 (★) は、再帰ツリーで発生する二種類のコスト

  1. 葉の合計コスト $\Theta(n^{\log_b a})$
  2. 分割・統合の合計コスト $\sum a^{j}f(n/b^{j})$

のどちらが優勢かで漸化式の挙動が決まると示唆している。これはマスター定理の三つのケースを理解するための土台となる。

Summary

補題 4.2 の要点:

漸化式 $T(n) = aT(n/b) + f(n)$ の解は、再帰ツリーの

  • 「葉の総コスト」$\Theta(n^{\log_b a})$
  • 「内部ノードの総コスト (分割・統合コストの総和)」$\sum a^j f(n/b^j)$

の和として表せる。

この補題は、マスター定理の3つのケースが、再帰ツリーのどの部分のコストが支配的になるかによって決まることを示唆している。

ケース 比較基準 再帰ツリーで支配的なコスト
1 $f(n)=O\!\bigl(n^{\log_b a-\varepsilon}\bigr)$（葉より「かなり小さい」） 葉レベルの合計コスト $\Theta\!\bigl(n^{\log_b a}\bigr)$
2 $f(n)=\Theta\!\bigl(n^{\log_b a}\bigr)$（葉と同じ程度） すべてのレベルが同じオーダーで並び、対数個ぶん積み重なる
3 $f(n)=\Omega\!\bigl(n^{\log_b a+\varepsilon}\bigr)$（葉より「かなり大きい」） 上位レベル（特に根付近）のコスト $f(n)$ が支配的

ここで $\varepsilon>0$ は「かなり」の定量化になっている。 補題 4.2 は再帰ツリーを

  • 葉の総コスト　$\Theta\!\bigl(n^{\log_b a}\bigr)$
  • 各レベルの分割・統合コストの総和　$\sum_{j=0}^{\lfloor\log_b n\rfloor} a^{j}f\!\bigl(n/b^{j}\bigr)$

の和に分解した。このどちらが大きいかを比較すれば、そのまま上の 3 ケースに対応する。

Note

分割するたびに掛かるコスト $f(n)$ と、部分問題が底まで分割されたときにまとめて現れる葉のコスト $n^{\log_b a}$ を比べるだけで、漸化式 $T(n)$ のオーダーが決まる。

  • $f(n)$ が葉コストより小さければ、末端（葉） が勝つ。

  • ほぼ同じなら、全レベルが肩を並べ、$\log n$ 倍に膨らむ。

  • $f(n)$ が葉コストより大きければ、最初の分割（根付近） がすべてを飲み込む。

    みたいなイメージだと思う。

和の漸近的評価 (補題 4.3)

次に、補題 4.2 で現れた和の項 $\sum_{j=0}^{\lfloor \log_b n \rfloor} a^j f(n/b^j)$ の漸近的な限界を評価する補題を見ていく。この補題の3つのケースが、マスター定理の3つのケースに直接対応する。

$$g(n) = \sum_{j=0}^{\lfloor \log_b n \rfloor} a^j f(n/b^j) \quad \quad (4.19)$$
補題 4.3

$$g(n) = \sum_{j=0}^{\lfloor \log_b n \rfloor} a^j f(n/b^j)$$

の漸近的な限界は以下のように特徴づけられる。

  1. ある定数 $\epsilon > 0$ に対して $f(n) = O(n^{\log_b a - \epsilon})$ ならば、$g(n) = O(n^{\log_b a})$
  2. ある定数 $k \ge 0$ に対して $f(n) = \Theta(n^{\log_b a} \lg^k n)$ ならば、$g(n) = \Theta(n^{\log_b a} \lg^{k+1} n)$
  3. ある定数 $c$ ($0 < c < 1$) と全ての $n \ge 1$ に対して $0 < af(n/b) \le cf(n)$ を満たすならば、$g(n) = \Theta(f(n))$

証明

ケース1 $f(n) = O(n^{\log_b a - \epsilon})$ であり、これは $f(n/b^j) = O((n/b^j)^{\log_b a - \epsilon})$ を意味する。これを式(4.19)に代入すると、

$$ \begin{align*} g(n) &= \sum_{j=0}^{\lfloor \log_b n \rfloor} a^j O\left(\left(\frac{n}{b^j}\right)^{\log_b a - \epsilon}\right) \\ &= O\left(\sum_{j=0}^{\lfloor \log_b n \rfloor} a^j \frac{n^{\log_b a - \epsilon}}{(b^j)^{\log_b a - \epsilon}}\right) \quad &\text{(章末問題3-5(c)を繰り返し適用)} \\ &= O\left(n^{\log_b a - \epsilon} \sum_{j=0}^{\lfloor \log_b n \rfloor} \frac{a^j}{(b^{\log_b a - \epsilon})^j}\right) \\ &= O\left(n^{\log_b a - \epsilon} \sum_{j=0}^{\lfloor \log_b n \rfloor} \left(\frac{ab^\epsilon}{b^{\log_b a}}\right)^j\right) \\ &= O\left(n^{\log_b a - \epsilon} \sum_{j=0}^{\lfloor \log_b n \rfloor} (b^\epsilon)^j\right) \quad &\text{(式(3.17) p.56より)} \\ &= O\left(n^{\log_b a - \epsilon} \left(\frac{b^{\epsilon(\lfloor \log_b n \rfloor + 1)} - 1}{b^\epsilon - 1}\right)\right) \quad &\text{(式(A.6) p.966より)} \end{align*} $$
$$b^{\epsilon(\lfloor \log_b n \rfloor + 1)} - 1 \le b^{\epsilon(\log_b n + 1)} = b^{\epsilon \log_b n} b^\epsilon = n^\epsilon b^\epsilon = O(n^\epsilon)$$

である。したがって、$g(n) = O(n^{\log_b a - \epsilon} \cdot n^\epsilon) = O(n^{\log_b a})$ となり、ケース1が証明される。

$$f(n/b^j) = \Theta((n/b^j)^{\log_b a} \lg^k (n/b^j))$$

となる。これを式(4.19)に代入し、章末問題3-5(c) を繰り返し適用すると、

$$ \begin{align*} g(n) &= \Theta\left(\sum_{j=0}^{\lfloor \log_b n \rfloor} a^j \frac{n^{\log_b a}}{(b^j)^{\log_b a}} \lg^k \left(\frac{n}{b^j}\right)\right) \\ &= \Theta\left(\sum_{j=0}^{\lfloor \log_b n \rfloor} \frac{a^j n^{\log_b a}}{a^j} \lg^k \left(\frac{n}{b^j}\right)\right) \\ &= \Theta\left(n^{\log_b a} \sum_{j=0}^{\lfloor \log_b n \rfloor} \lg^k \left(\frac{n}{b^j}\right)\right) \\ &= \Theta\left(n^{\log_b a} \sum_{j=0}^{\lfloor \log_b n \rfloor} \left(\frac{\log_b (n/b^j)}{\log_b 2}\right)^k\right) \quad &\text{(式(3.19) p.56より)} \\ &= \Theta\left(n^{\log_b a} \sum_{j=0}^{\lfloor \log_b n \rfloor} \left(\frac{\log_b n - j}{\log_b 2}\right)^k\right) \quad &\text{(式(3.17), (3.18), (3.20)より)} \\ &= \Theta\left(\frac{n^{\log_b a}}{(\log_b 2)^k} \sum_{j=0}^{\lfloor \log_b n \rfloor} (\log_b n - j)^k\right) \\ &= \Theta\left(n^{\log_b a} \sum_{j=0}^{\lfloor \log_b n \rfloor} (\log_b n - j)^k\right) \quad & (b > 1 \text{ と } k \text{ は定数})\end{align*} $$

$\Theta$記法内の和は、次のように上から抑えられる。

$$ \begin{align*} \sum_{j=0}^{\lfloor \log_b n \rfloor} (\log_b n - j)^k &\le \sum_{j=0}^{\lfloor \log_b n \rfloor} ((\lfloor \log_b n \rfloor + 1) - j)^k \\ &= \sum_{i=1}^{\lfloor \log_b n \rfloor+1} i^k \quad &\text{(インデックス変更 p.968)} \\ &= O((\lfloor \log_b n \rfloor + 1)^{k+1}) \quad &\text{(練習問題 A.1-5 p.969)} \\ &= O(\log_b^{k+1} n) \quad &\text{(練習問題 3.3-3 p.59)} \end{align*} $$

練習問題 4.6-1 は、この和が同様に下から $\Omega(\log_b^{k+1} n)$ で抑えられることを示している。したがって、上下からタイトに抑えられるため、この和は $\Theta(\log_b^{k+1} n)$ である。

これから、$g(n) = \Theta(n^{\log_b a} \log_b^{k+1} n)$ と結論付けられ、$\log_b^{k+1} n = (\lg^{k+1} n) / (\lg b)^{k+1}$ であり、$\lg b$ は定数なので、$\Theta(n^{\log_b a} \lg^{k+1} n)$ となる。ケース2が完了した。

ケース3 $f(n)$ は $g(n)$ の定義式(4.19) ($j=0$ のとき) に現れ、$g(n)$ の全ての項は非負であることに注意する。すると、$g(n) = \Omega(f(n))$ である。

残るは $g(n) = O(f(n))$ を証明することだけである。不等式 $af(n/b) \le cf(n)$ を $j$ 回繰り返し適用すると、$a^j f(n/b^j) \le c^j f(n)$ が得られる。これを式(4.19)に代入すると、

$$ \begin{align*} g(n) &= \sum_{j=0}^{\lfloor \log_b n \rfloor} a^j f(n/b^j) \\ &\le \sum_{j=0}^{\lfloor \log_b n \rfloor} c^j f(n) \\ &\le f(n) \sum_{j=0}^{\infty} c^j \\ &= f(n) \left(\frac{1}{1-c}\right) \quad &\text{(式(A.7) p.967より、$|c|<1$ なので)} \\ &= O(f(n)) \end{align*} $$

したがって、$g(n) = \Theta(f(n))$ と結論付けられる。ケース3が証明され、補題全体の証明が完了する。

（証明終わり）☑️

以上で3つの場合すべてについて示したとおり、$g(n)$ の漸近的振る舞いは

  • $f(n)$ の成長速度
  • 正則性条件

によって決定される。補題 4.3 はこの事実を形式化し、マスター定理の3ケースに直接対応させている。

連続マスター定理の証明 (定理 4.4)

いよいよ、これらの補題を使って連続マスター定理を証明する。連続マスター定理は、補題 4.2 がベースケースを $0 \le n < 1$ としていたのに対し、より一般的なベースケース $0 < n < n_0$ ($n_0 > 0$ は任意の閾値定数) を扱う。

定理 4.4 (連続マスター定理 Continuous master Theorem)

$$T(n) = aT(n/b) + f(n)$$

の漸近的な挙動は以下のように特徴づけられる：

  1. ある定数 $\epsilon > 0$ に対して $f(n) = O(n^{\log_b a - \epsilon})$ ならば、$T(n) = \Theta(n^{\log_b a})$
  2. ある定数 $k \ge 0$ に対して $f(n) = \Theta(n^{\log_b a} \lg^k n)$ ならば、$T(n) = \Theta(n^{\log_b a} \lg^{k+1} n)$
  3. ある定数 $\epsilon > 0$ に対して $f(n) = \Omega(n^{\log_b a + \epsilon})$ であり、かつ、$f(n)$ が正則条件 $af(n/b) \le cf(n)$ (ある定数 $c<1$ と十分大きな全ての $n$ に対して) を満たすならば、$T(n) = \Theta(f(n))$

証明：式(4.18)の総和評価

アイデアは、補題4.3を適用して補題4.2の式(4.18)の総和を評価することだ。

このマスター定理の証明は、基本的には補題4.2で漸化式を展開し、その展開された形（特に総和の部分）を補題4.3を用いて評価するという方針で進められる。

しかし、既存の補題を適用する際には注意点がある。補題4.2は、漸化式の再帰が停止する基底ケースとして、$n$ がある特定の値 $n_1$ より小さい範囲 ($0 < n < n_1$) を想定している。一方で、このマスター定理では、基底ケースは $n$ が任意の閾値定数 $n_0$ より小さい範囲 ($0 < n < n_0$, $n_0 > 0$) であると暗黙的に仮定している。この $n_1$ と $n_0$ が一致するとは限らないため、補題4.2を直接適用するには工夫が必要となる。

また、僕たちが扱っているのはアルゴリズムの実行時間に関する漸化式（アルゴリズム的漸化式）なので、入力サイズ $n$ がある閾値 $n_0$ 未満の非常に小さい場合には、実行時間は定数 $\Theta(1)$ とみなせる。したがって、駆動関数 $f(n)$ の性質（非負であることなど）は、$n \ge n_0$ の範囲で定義され、満たされていれば十分であると仮定できる。

この準備と注意点を踏まえ、この定理の証明では、基底ケースの不一致を解消し、補題を適用しやすくするために、まず補助関数を導入する。

$$ \begin{aligned} T'(n) &= T(n_0 n) \\ &= \begin{cases} \Theta(1) & \text{if } n_0 n < n_0 \text{ ,} \\ aT(n_0 n/b) + f(n_0 n) & \text{if } n_0 n \ge n_0 \text{ .} \end{cases} \\ &= \begin{cases} \Theta(1) & \text{if } n < 1 \text{ ,} \\ aT'(n/b) + f'(n) & \text{if } n \ge 1 \text{ .} \end{cases} \quad (4.20) \end{aligned} $$
$$ T'(n) = \Theta(n^{\log_b a}) + \sum_{j=0}^{\lfloor \log_b n \rfloor -1} a^j f'(n/b^j) \quad (4.21) $$

$T'(n)$ を解くために、まず $f'(n)$ を評価する。定理の個々のケースを調べてみよう。

$$ \begin{aligned} f'(n) &= f(n_0 n) \\ &= O((n_0 n)^{\log_b a - \epsilon}) \\ &= O(n_0^{\log_b a - \epsilon} \cdot n^{\log_b a - \epsilon}) \\ &= O(n^{\log_b a - \epsilon}) \end{aligned} $$

となる。なぜなら、$n_0, \log_b a, \epsilon$ は定数なので、$n_0^{\log_b a - \epsilon}$ も定数だからだ。

$$ \begin{aligned} T(n) &= T'(n/n_0) \\ &= \Theta(((n/n_0))^{\log_b a}) + O(((n/n_0))^{\log_b a}) \\ &= \Theta(n^{\log_b a} / n_0^{\log_b a}) + O(n^{\log_b a} / n_0^{\log_b a}) \\ &= \Theta(n^{\log_b a}) + O(n^{\log_b a}) \quad (\text{問題 3-5(b)により定数係数は吸収される}) \\ &= \Theta(n^{\log_b a}) \end{aligned} $$

となり、定理のケース1が完了します。

$$ \begin{aligned} f'(n) &= f(n_0 n) \\ &= \Theta((n_0 n)^{\log_b a} \lg^k (n_0 n)) \\ &= \Theta(n_0^{\log_b a} n^{\log_b a} (\lg n_0 + \lg n)^k) \\ &= \Theta(n^{\log_b a} \lg^k n) \quad (\text{定数項 } n_0^{\log_b a} \text{ と } \lg n_0 \text{ の影響は } \Theta \text{ 記法で吸収される}) \end{aligned} $$

となる。

$$ \begin{aligned} T(n) &= T'(n/n_0) \\ &= \Theta(((n/n_0))^{\log_b a}) + \Theta(((n/n_0))^{\log_b a} \lg^{k+1} (n/n_0)) \\ &= \Theta(n^{\log_b a}) + \Theta(n^{\log_b a} \lg^{k+1} n) \quad (\text{問題 3-5(c)により定数項は吸収される}) \\ &= \Theta(n^{\log_b a} \lg^{k+1} n) \end{aligned} $$

となり、定理のケース2が証明される。原文では第1項が最終結果に吸収されることを利用し $\Theta((n/n_0)^{\log_b a} \lg^{k+1} (n/n_0))$ としているが、ここでは式(4.21)の形をより直接的に反映した。最終結果は同じ。

$$ \begin{aligned} f'(n) &= f(n_0 n) \\ &= \Omega((n_0 n)^{\log_b a + \epsilon}) \\ &= \Omega(n^{\log_b a + \epsilon}) \end{aligned} $$

となる。

$$ \begin{aligned} af'(n/b) &= af(n_0 (n/b)) \\ &= af((n_0 n)/b) \end{aligned} $$
$$ \begin{aligned} af((n_0 n)/b) &\le cf(n_0 n) \\ &= cf'(n) \end{aligned} $$

したがって、$af'(n/b) \le cf'(n)$ となり、$f'(n)$ は補題4.3のケース3の要件を満たす。

$$ \begin{aligned} T(n) &= T'(n/n_0) \\ &= \Theta(((n/n_0))^{\log_b a}) + \Theta(f'(n/n_0)) \end{aligned} $$
$$ \begin{aligned} T(n) &= \Theta(f'(n/n_0)) \\ &= \Theta(f(n_0 \cdot (n/n_0))) \\ &= \Theta(f(n)) \end{aligned} $$

となり、定理のケース3が完了し、したがって定理全体が完了する。

（証明終わり）☑️

ここまでのまとめ

補題 4.2（再帰ツリー表現）

$$ T(n)=a\,T\bigl(\tfrac n b\bigr)+f(n) $$
$$ T(n)=\Theta\bigl(n^{\log_b a}\bigr)+\sum_{j\ge0}a^j\,f\bigl(n/b^j\bigr) $$

と表す。

補題 4.3（和項の評価）

$\sum a^j f(n/b^j)$ を、次の３つのケースに応じて評価し、

  1. 葉支配：  $f(n)=O\bigl(n^{\log_ba-\varepsilon}\bigr)$
  2. 拮抗：      $f(n)=\Theta\bigl(n^{\log_ba}\bigr)$
  3. 内部ノード支配： $f(n)=\Omega\bigl(n^{\log_ba+\varepsilon}\bigr)$

各場合に対応する漸近解を導出した。

定理 4.4（一般的なベースケースへの拡張）

$$ n'=n/n_0 $$

を導入。変換後の漸化式に 補題 4.2 を適用し、補題 4.3 で和項を評価することで、３つのケース別の解を得る。

再帰ツリー上で

  1. 葉（$\Theta(n^{\log_ba})$）
  2. 内部ノード（$\sum a^j f(n/b^j)$）

のどちらがコストを支配するか、あるいは両者が同程度に寄与するか、という視点からマスター定理の３ケースを直感的に理解できる。

練習問題

練習問題4.6-1

次式が成立することを示せ。

$$\sum_{j=0}^{\lfloor \log_b n \rfloor} (\log_b n - j)^k = \Omega (\log_{b}^{k+1} n)$$
$$ m = \Bigl\lfloor \log_b n\Bigr\rfloor $$

とおく。すると $\log_b n \ge m$ かつ $\log_b n < m+1$ である。

$$ \sum_{j=0}^{\lfloor\log_b n\rfloor}(\log_b n - j)^k \;\ge\; \sum_{j=0}^{m}(m - j)^k \;=\; \sum_{i=0}^{m} i^k $$

右辺では，$\log_b n - j \ge m-j$ を使った。

$$ \sum_{i=0}^{m} i^k \;\ge\; \int_{0}^{m} x^k\,dx \;=\; \frac{m^{k+1}}{k+1} $$
$$ \sum_{j=0}^{\lfloor\log_b n\rfloor}(\log_b n - j)^k \;\ge\; \frac{m^{k+1}}{k+1} $$

最後に $m=\lfloor\log_b n\rfloor$ と $\log_b n$ は定数ずれしかないので

$$ m\;=\;\Theta(\log_b n) \quad\Longrightarrow\quad m^{k+1}=\Theta\bigl((\log_b n)^{k+1}\bigr) $$
$$ \sum_{j=0}^{\lfloor\log_b n\rfloor}(\log_b n - j)^k \;=\;\Omega\bigl((\log_b n)^{k+1}\bigr) $$

（証明おわり）☑️

Akra-Bazzi 漸化式

Akra-Bazzi漸化式とは何か？

Akra-Bazzi漸化式は、複雑な分割統治アルゴリズムの実行時間を解析するための強力な数学的ツールである。

Akra-Bazzi漸化式の定義

Akra-Bazzi漸化式は、以下の形式で表される。

Akra-Bazzi漸化式の定義

$$T(n) = f(n) + \sum_{i=1}^k a_i T(n/b_i) \tag{4.22}$$

ここで、

  • $k$ は正の整数である。
  • 定数 $a_1, a_2, \dots, a_k \in \mathbb{R}$ はすべて厳密に正である ($a_i > 0$)
  • 定数 $b_1, b_2, \dots, b_k \in \mathbb{R}$ はすべて厳密に1より大きい ($b_i > 1$)
  • 駆動関数 (driving function) $f(n)$ は、十分に大きな非負の実数 $n$ 上で定義され、それ自体も非負である ($f(n) \ge 0$ )

Akra-Bazzi漸化式の意義とマスター定理との比較

何がうれしいのか？

Akra-Bazzi漸化式は、マスター定理が扱える漸化式のクラスを一般化したものである。

  • マスター定理: 問題をほぼ同じサイズのサブ問題に分割するアルゴリズムの実行時間を解析するのに適している。例えば、$T(n) = aT(n/b) + f(n)$ のような形。
  • Akra-Bazzi漸化式: 問題を異なるサイズのサブ問題に分割するアルゴリズムの実行時間を記述できる。例えば、$T(n) = T(n/3) + T(2n/3) + O(n)$ のような場合。
Akra-Bazzi漸化式の利点

マスター定理では扱えない、より複雑で現実的な分割統治アルゴリズム（サブ問題のサイズが不均等）の解析を可能にする点が、Akra-Bazzi漸化式の大きな利点である。

しかし、Akra-Bazzi法を適用してこの漸化式を解く際には、床関数 $\lfloor x \rfloor$ や天井関数 $\lceil x \rceil$ の扱いに関して、マスター定理よりも注意深い考察が必要となる。

床関数・天井関数の取り扱いと多項式増加条件

アルゴリズムは通常、整数サイズの入力を扱うが、漸化式の数学的解析は実数で行う方が便利な場合が多い。このギャップを埋めるために、床関数や天井関数が登場するが、これらが解析を複雑にすることがある。

なぜ床関数・天井関数が問題になるのか？

漸化式で $n/b_i$ のような項が現れる際、入力 $n$ が整数であっても $n/b_i$ が整数になるとは限らない。そのため、厳密には $T(\lfloor n/b_i \rfloor)$ や $T(\lceil n/b_i \rceil)$ のように記述する必要がある。

目的: 厳密さを保ちつつ、床関数や天井関数の影響を実用的な範囲で簡略化して扱いたい。最終的な目標はアルゴリズムの挙動の本質を理解することであり、数学的に細かい面倒な問題に囚われないようにしたい。

数学的には、駆動関数 $f(n)$ が特殊な振る舞いをする場合、床関数や天井関数の存在が解の漸近的な挙動に影響を与える可能性がある。そのため、一般的にはこれらを単純に無視することはできない。しかし、幸いなことに、アルゴリズム解析で現れる多くの駆動関数 $f(n)$ は「行儀が良い」ため、これらの関数を無視しても問題ないことが多い。

多項式増加条件

駆動関数 $f(n)$ が「行儀が良い」ことを保証するための条件が、多項式増加条件 (polynomial-growth condition) である。

多項式増加条件の定義

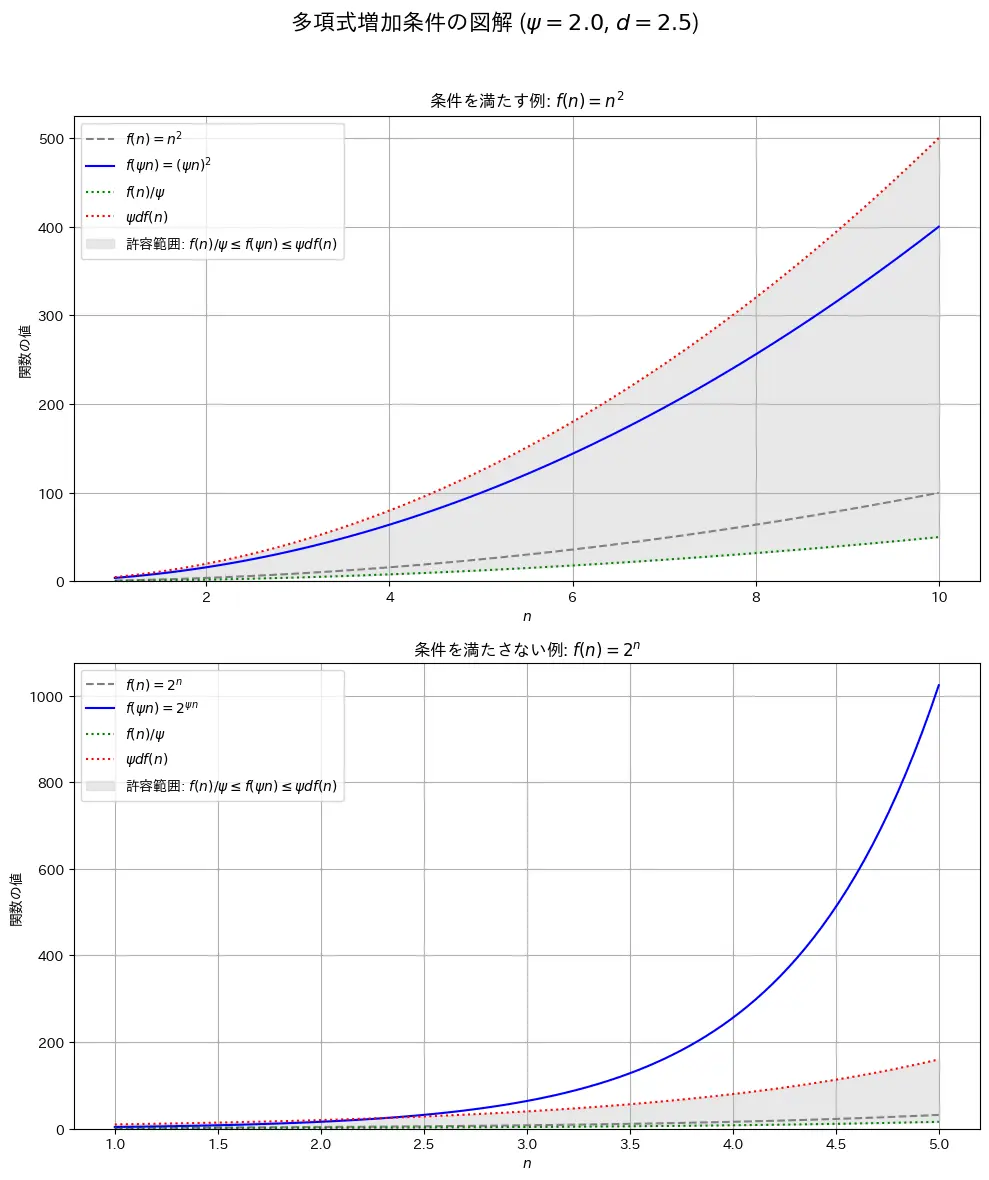
十分に大きなすべての正の実数で定義された関数 $f(n)$ は、次のような定数 $\hat{n} > 0$ が存在する場合に多項式増加条件を満たす。任意の定数 $\phi \ge 1$ に対して、定数 $d > 1$（$\phi$ に依存する）が存在し、すべての $1 \le \psi \le \phi$ および $n \ge \hat{n}$ に対して以下が成り立つ。

$$ f(n)/\psi \le f(\psi n) \le \psi d f(n) $$

この定義は少々複雑に見えるかもしれないが、大まかには「$f(n)$ が入力 $n$ の定数倍の変化に対して、その値も（ある範囲の）定数倍の変化に収まる」という性質、$f(\Theta(n)) = \Theta(f(n))$ に近いことを意味する。

実際には、多項式増加条件はこれよりも若干強い条件である。（練習問題4.7-4参照）また、この条件は $f(n)$ が漸近的に正であることも含意する。（練習問題4.7-3参照）

多項式増加条件を満たす関数の例:

  • $f(n) = \Theta(n^\alpha \log^\beta n \log \log^\gamma n)$ の形の関数（$\alpha, \beta, \gamma$ は定数）
  • 多くの多項式的に有界な関数がこれに該当する

多項式増加条件を満たさない関数の例:

  • 指数関数（例：$2^n$）や超指数関数（例：$n!$）
  • 多項式的に有界であってもこの条件を満たさない関数も存在する（練習問題4.7-2参照）

多項式増加条件がもたらす恩恵：定理4.5

駆動関数 $f(n)$ が多項式増加条件を満たす場合、Akra-Bazzi漸化式における床関数や天井関数の存在は、解の漸近的な挙動に影響を与えない。

定理 4.5 (床関数・天井関数の影響)

非負の実数上で定義され、漸化式(4.22)を満たす関数を $T(n)$ とし、ここで $f(n)$ は多項式増加条件を満たすと仮定する。$T'(n)$ を自然数上で定義された別の関数とし、各 $T(n/b_i)$ が $T(\lfloor n/b_i \rfloor)$ または $T(\lceil n/b_i \rceil)$ のいずれかで置き換えられる点を除いて、同じく漸化式(4.22)を満たすとする。このとき、$T'(n) = \Theta(T(n))$ である。

何がうれしいのか？ この定理により、駆動関数 $f(n)$ が多項式増加条件を満たしていれば、解析の便宜上、床関数や天井関数を無視して議論を進めることが正当化される。これにより、漸化式の取り扱いが大幅に簡略化される。

さらに、床関数や天井関数による引数のブレ（高々1の差）だけでなく、より大きなブレ、$|h_i(n)| = O(n/\log^{1+\epsilon} n)$（ある定数 $\epsilon > 0$, 十分大きな $n$）についても駆動関数が多項式増加条件を満たす限り、$T(nb_i)$ の任意の項を $T(n/b_i + h_i(n))$ で置き換えても漸近的な解に影響がないことが知られている。

これは、分割統治アルゴリズムにおける実際の分割が多少粗くても、その実行時間の漸近的なオーダーは変わらないことを意味する。

Akra-Bazzi法による漸化式の解法

Akra-Bazzi法は、Akra-Bazzi漸化式(4.22)を解くために開発された手法である。定理4.5のおかげで、駆動関数が多項式増加条件を満たせば、床関数・天井関数が存在する場合や、前述のようなより大きなブレ（摂動？言葉あってるか曖昧）がある場合にも適用できる。

Akra-Bazzi法の概要

Akra-Bazzi法による解法は、主に以下の2つのステップからなる。

  1. 特性指数 $p$ の決定: まず、次の式を満たす唯一の実数 $p$ を見つける。
  2. 解の導出: $p$ を用いて、漸化式の解を積分形式で求める。

ステップ1: 特性指数 $p$ の決定

特性指数 $p$ の決定式

次の方程式を満たす実数 $p$ を求める。

$$\sum_{i=1}^k \frac{a_i}{b_i^p} = 1$$

このような $p$ は常に一意に存在する。なぜなら、$g(p) = \sum_{i=1}^k a_i/b_i^p$ とおくと、$a_i > 0, b_i > 1$ より、$g(p)$ は $p$ に関して連続な単調減少関数であり、$p \to -\infty$ のとき $g(p) \to \infty$、$p \to \infty$ のとき $g(p) \to 0$ となるため、中間値の定理により $g(p)=1$ となる $p$ がただ一つ存在する。

ステップ2: 解の導出

上記で求めた $p$ を用いて、Akra-Bazzi漸化式(4.22)の解は次のように与えられる。

Akra-Bazzi法の解の公式

$$T(n) = \Theta \left( n^p \left( 1 + \int_1^n \frac{f(x)}{x^{p+1}} dx \right) \right)\tag{4.23}$$

何がうれしいのか？ この公式 (4.23) を使うことで、複雑な形のAkra-Bazzi漸化式の解の漸近的なオーダー（$\Theta$記法）を求めることができる。

テストに出るよ～＼_(・ω・`)

具体例：漸化式 $T(n) = T(n/5) + T(7n/10) + n$ の解法

Akra-Bazzi法を用いた漸化式の解法例

次の漸化式を考える。

$$T(n) = T(n/5) + T(7n/10) + n\tag{4.24}$$

この漸化式は、ある選択アルゴリズム（$n$ 個の要素から $i$ 番目に小さい要素を見つけるアルゴリズム、セクション9.1参照）の解析で登場する。

1. パラメータの特定:

漸化式(4.22)と比較すると、

  • $k=2$
  • $a_1=1, a_2=1$
  • $b_1=5, b_2=10/7$
  • $f(n)=n$ 駆動関数 $f(n)=n$ は多項式増加条件を満たす（例えば $f(n) = n^1 \log^0 n$ と考えられる）

2. 特性指数 $p$ の決定: 次の方程式を満たす $p$ を求める。

$$\frac{1}{5^p} + \frac{1}{(10/7)^p} = 1 \quad \text{すなわち} \quad \left(\frac{1}{5}\right)^p + \left(\frac{7}{10}\right)^p = 1$$

この $p$ を正確に求めるのは難しいが、$p \approx 0.83978 \dots$ である。 しかし、正確な値が分からなくても解ける場合がある。

  • $p=0$ のとき: $(1/5)^0 + (7/10)^0 = 1+1 = 2 > 1$
  • $p=1$ のとき: $(1/5)^1 + (7/10)^1 = 1/5 + 7/10 = 2/10 + 7/10 = 9/10 < 1$

関数 $g(p) = (1/5)^p + (7/10)^p$ は $p$ について単調減少なので、$0 < p < 1$ であることがわかる。この情報が重要となる。

3. 解の導出:

公式(4.23)に $f(x)=x$ を代入する。

$$T(n) = \Theta \left( n^p \left( 1 + \int_1^n \frac{x}{x^{p+1}} dx \right) \right)$$

積分のところを計算する。

$$\int_1^n \frac{x}{x^{p+1}} dx = \int_1^n x \cdot x^{-(p+1)} dx = \int_1^n x^{1-(p+1)} dx = \int_1^n x^{-p} dx$$

ここで、$0 < p < 1$ より、$1-p > 0$ であり、特に $p \neq 1$ なので $-p \neq -1$ である。 積分公式 $\int x^k dx = \frac{x^{k+1}}{k+1}$ ($k \neq -1$) を用いると、

$$\int_1^n x^{-p} dx = \left[ \frac{x^{-p+1}}{-p+1} \right]_1^n = \frac{n^{1-p}}{1-p} - \frac{1^{1-p}}{1-p} = \frac{n^{1-p}}{1-p} - \frac{1}{1-p}$$

よって、

$$\begin{aligned}T(n) &= \Theta \left( n^p \left( 1 + \frac{n^{1-p}}{1-p} - \frac{1}{1-p} \right) \right) \\\end{aligned}$$

ここで、$1-p$ は正の定数であるため、括弧内の主要項は $\frac{n^{1-p}}{1-p}$ である。 したがって、

$$1 + \frac{n^{1-p}}{1-p} - \frac{1}{1-p} = \Theta(n^{1-p})$$

となる。ゆえに、

$$\begin{aligned}T(n) &= \Theta \left( n^p \cdot \Theta(n^{1-p}) \right) \\ &= \Theta (n^p \cdot n^{1-p}) \quad (\text{$\Theta$記法の性質より}) \\ &= \Theta (n^{p + (1-p)}) \\ &= \Theta (n^1) \\ &= \Theta(n) \end{aligned}$$

（最後のステップは問題 3-5(d)による、と元テキストでは参照されているが、$\Theta$記法の積の性質 $\Theta(g(n)) \cdot \Theta(h(n)) = \Theta(g(n)h(n))$ から導かれる。）

したがって、漸化式(4.24)の解は $T(n) = \Theta(n)$ である。

まとめ：Akra-Bazzi法とマスター定理

Akra-Bazzi法とマスター定理の比較

  • 一般性: Akra-Bazzi法はマスター定理よりも一般的であり、サブ問題のサイズが不均等な分割統治アルゴリズムの解析にも適用できる。
  • 複雑さ: Akra-Bazzi法の適用には、微積分の計算や、時には $p$ の値を推論する作業が必要となる。
  • 床関数・天井関数: 床関数や天井関数を無視するためには、駆動関数 $f(n)$ が多項式増加条件を満たすことを確認する必要がある。
  • 使いやすさ: マスター定理が適用できる場合（サブ問題のサイズがほぼ等しい場合）は、マスター定理の方が使いやすい。

Akra-Bazzi法とマスター定理は、どちらもアルゴリズムの実行時間解析、特に分割統治法に基づくアルゴリズムの解析において非常に有用なツールである。それぞれの特性を理解し、状況に応じて適切な手法を選択することが重要である。

練習問題

練習問題4.7-2

$f(n)=n^2$ は多項式増加条件を満足し、$f(n)=2^n$ は満足しないことを示せ。

(1) $f(n)=n^2$ が多項式増加条件を満足すること

$$ f(n) = n^2 \le 1\cdot n^2 \quad\Longrightarrow\quad n^2 = O(n^2) $$

よって、$f(n)=n^2$ は多項式増加条件（次数 $k=2$）を満たす。

(2) $f(n)=2^n$ が多項式増加条件を満たさないこと

$$ 2^n \;\le\; C\,n^k $$

が成立していなければならない。しかし、次の事実からこれは成り立たない。

$$ \lim_{n\to\infty}\frac{2^n}{n^k} = \infty $$

すなわち $2^n$ はいかなる $n^k$ よりも漸近的に速く大きくなる。

増加率の議論

数列 $a_n = 2^n/n^k$ の項間比を考えると、

$$ \frac{a_{n+1}}{a_n} = \frac{2^{n+1}/(n+1)^k}{2^n/n^k} = 2\Bigl(\tfrac{n}{n+1}\Bigr)^k \;\xrightarrow[n\to\infty]{}\; 2 \gt 1 $$

ゆえに十分大きな $n$ 以降は単調増加して $a_n\to\infty$ し、任意の定数 $C$ をも超えてしまう。

したがって、$2^n$ を任意の多項式 $n^k$ で抑えることはできず、「多項式増加条件」を満たさない。

以上により、

  • $f(n)=n^2$ は多項式増加条件を満たす。
  • $f(n)=2^n$ は多項式増加条件を満たさない。

ことが示された。

全体のまとめ

  • 漸化式を解くために以下の2つの方法があることを見た
    • マスター法
    • Akra Bazzi法
  • それぞれに対して以下の3つを確認した
    • 適用できる条件（マスター法の3つのケース・Akra Bazzi法の多項式増加条件）
    • 数学的な背景（連続マスター定理・定理4.5）
    • 適用方法（具体例を使って確認した）
  • 分割統治法の実行時間の漸近的なオーダーを求めることができるようになった！