以下は私が作成した『アルゴリズムイントロダクション 第4版』の輪読資料です。一部、練習問題や章末問題を解いた結果も載せています。

第２章：さあ、始めよう Part2

アルゴリズムの解析

解析するとはなにか？

同じ問題を解く複数のアルゴリズムがあるとき、どれを採用するのかを考えよう。このとき重要なのは、アルゴリズムを解析して優劣を決めて選択することだ。解析するとはなにか？

🔵Important

アルゴリズムの実行に必要な資源量を予測することを、アルゴリズムを解析するという。

第１章では、アルゴリズムの効率が良いとはどういう意味か？という内容を扱った。そこでは、主に以下の２つの観点があると述べた。

🔘Note

  • 時間効率（実行時間が速いか遅いか）
  • 空間効率（使用するメモリ領域が大きいか小さいか）

実はこれ以外にも考慮したい資源量はある。たとえば、

  • 通信バンド領域
  • エネルギー消費量

などだ。考慮すべき資源量の優先順位は、アルゴリズムが適用される実問題が抱える制約条件に応じて変わる。

たとえば、通信設備が不十分で帯域がすごく狭い国でのオンライン診療のためのシステムを構築するのであれば、通信バンド領域は考慮する優先順位の高い資源量になるし、電気インフラの不十分な国で信号機を制御するシステムを作るのであればエネルギー消費量の優先順位が高くなる。あるいはそもそも電気インフラが弱いのであれば、一時的な停電に対してロバストなシステムであることのほうが優先順位として高いかもしれない。個別具体の問題に応じて考慮されるべき資源量は変わる。

とはいえ、多くの場合考慮される資源量となるのは主に「計算時間」ではある。ではその計算時間をどのように測ればよいのか？

実際にコーディングをしてコンピュータに計算させて測ればよいのか？

これは測定方法の一つではあるが、あまり良い方法ではない。なぜなら実装するプログラミング言語に応じて実行時間が変わるし、使用するコンピュータの性能に応じても変化するからだ。公正な比較にならない。

公正な比較をするにはどうすればいいのか？

現実のコンピュータが行っている処理をモデル化し、その設定の中で計算時間を定義すれば公正な比較になる。

🔵Important

本書の多くの部分では、汎用の単一プロセッサの計算モデルであるランダムアクセスマシン (RAM) を実装技術として仮定し、アルゴリズムはコンピュータプログラムとして実現する。

RAM モデルの特徴をざっくりと説明しよう。

  1. RAM モデルでは命令は1つずつ逐次的に実行される
  2. 並行演算は存在しない
  3. どの命令も同じ計算時間がかかる

3についてもう少し詳しく言うと、

  • 変数の値を利用する
  • 変数へ値を格納する

このどの命令も同じ定数時間がかかると仮定している。

厳密な RAM モデルの定義については扱わない。ただ、RAM モデルが実行できる命令の定義の仕方には注意が必要だ。

「任意の問題に対して常に最適な解を定数時間で計算する」のような魔法の命令を持っている神様コンピュータとして RAM を定義すると、あまりに現実から乖離するからだ。

ということで、なるべく実際のコンピュータが共通に持っている命令をもとにして RAM モデルの定義の指針とする。

RAM モデルをざっくり定義する

では、RAM モデルが持っている命令群を定義する。

🔵Important RAM モデルが持っている命令群

  • 算術演算
    • 加算
    • 減算
    • 乗算
    • 除算
    • 剰余
    • 切り捨て
    • 切り上げ
  • データ移動
    • ロード
    • ストア
    • コピー
  • 制御
    • 条件付き分岐
    • 無条件分岐
    • サブルーチンの呼び出し
    • サブルーチンからの復帰

また、RAM モデルが利用できるデータ型は以下の通り。

  • 整数
  • 浮動小数点数
  • 文字

この本では浮動小数点数の桁数（精度）について深入りしないが、実際のアプリケーションでは精度が極めて重要になることも多い。

🔘Note 浮動小数点の精度の補足

10 進数の 0.1 は 2 進数では無限循環小数になるため、 IEEE 754 単精度 (32 bit) でも倍精度 (64 bit) でも 厳密な 0.1 は表現できません。したがって 0.1 + 0.2 == 0.3 が FALSE になることがあります。これは「精度が重要」という指摘の背景にある典型例だと思います。

このことについて説明した Zenn や Qiita の記事で以下のようなものもあります。

また、メモリ上の 1 ワードにはビット数に上限があると仮定する。入力サイズを $n$ とするとき、整数は通常 $c \log_2 n$ ビット（定数 $c \geq 1$）で表現できるとする。

$c$ を 1 以上にするのは、配列の添字として最大値 $n$ を格納できる大きさを確保するためであり、$c$ を定数に制限するのは、ワード長が恣意的に大きくなってしまうのを防ぐためだ。もしワード長を無制限に伸ばせるなら、1 ワードに莫大な量のデータを詰めこみ、それを「定数時間」で処理できてしまう。しかし、これは現実的とは言えない。

RAM モデルのグレーゾーンな話題

ビットシフトについて

実際のコンピュータには、前述していない命令も含まれており、そうした命令は RAM モデルではグレーゾーンに当たる。

Example

たとえば、冪乗演算は定数時間の命令とみなせるだろうか？

この問いに対する一般の場合における答えは、「いいえ」になる。

整数 $x$ と $n$ に対して $x^n$ を計算するには、通常 $n$ の対数時間がかかる（式 (31.34) を参照）。また、結果が 1 語に収まるかどうかも気にする必要がある。したがって、定数時間の命令とはみなせない。

しかし、$n$ が $2$ の冪であれば、冪乗演算を定数時間操作と見なせることが多い。なぜなら、多くのコンピュータには〈左シフト〉命令があり、一定時間で整数のビット列を n ビット左にずらせるからだ。

ほとんどのコンピュータでは、ビットを $1$ ビット左にずらす操作は $2$ 倍に相当するため、$n$ ビット左にずらすのは $2^n$ 倍と同じことだ。したがって、語長以内の $n$ であれば、整数 $1$ を $n$ ビット左にシフトする 1 回の定数時間命令で $2^n$ を計算できる。この本ではこうしたグレーゾーンを避け、結果が 1語に収まる限り $2^n$ の計算や $2^n$ 倍の乗算を定数時間操作として扱う。

🔘Note ビットシフトの補足

コンピュータが扱う整数は固定長の ビット列（例：32 bit や 64 bit）で表されます。ビットシフトは、このビット列を左あるいは右に $n$ ビット分ずらし、空いた部分を 0（あるいは符号ビット）で埋める単純なビット列操作のことです。

例：0110 (22) を $1$ ビット左シフトすると 1100 (44) となり、確かに $22\times2^1 = 44$ になっていますね。

現代 CPU には バレルシフタ (barrel shifter) と呼ばれる回路が組み込まれており、 ハードウェア的に 1 クロックで処理されているようになっているみたいです。

メモリ階層について

RAM モデルは、現代のコンピュータで一般的な以下のようなメモリ階層をモデルとして考慮していない。

  • キャッシュ
  • 仮想メモリ

🔘Note キャッシュと仮想メモリの補足

実機のプロセッサは

  1. CPU レジスタ
  2. キャッシュ
  3. 主記憶 (DRAM)
  4. 補助記憶 (SSD/HDD)

という 階層構造 でデータを扱います。階層が下がるほど容量は大きく、レイテンシと消費電力 は増大します。RAM モデルが仮定する「すべてのメモリアクセスが等コスト」というのはこのような実機のプロセッサをかなり単純化したものになります。

実際のプログラムでは、メモリ階層の影響が顕著になる場合があり、それを捉えるための別の計算モデルもいくつか提案されている。この本では 11.5 節といくつかの問題でメモリ階層の影響を扱うが、おおむね解析では考慮しない。理由は以下の二つ。

  • メモリ階層を含むモデルは RAM モデルよりかなり複雑で扱いづらい
  • RAM モデルでの解析結果は多くの場合、実機での性能を非常によく予測できる

RAM モデルの話おわり。

挿入ソートの解析

計算時間の数え方

さて、I​NSERTION-SORT 手続きを例にとってアルゴリズムの解析を行ってみよう。注目する資源量は計算時間だ。この手続きを実行するのにかかる時間はどれくらいなのだろうか？

復習：
INSERTION-SORT(A,n)

1.for i = 2 to n
2.    key = A[i]
3.    // A[i] をソート済みの部分配列 A[1:i-1] に挿入する
4.    j = i - 1
5.    while j > 0 かつ A[j] > key
6.        A[j+1] = A[j]
7.        j = j - 1
8.    A[j+1] = key

「解析するとはなにか？」で言ったことの繰り返しになるが、実際に自分のコンピュータで動かし実行時間を測定するとなると、

  • 実装言語
  • コンパイラ／インタプリタの最適化
  • CPU やメモリ構成
  • 同時に動いている他タスク

といった「たまたまの環境」に強く縛られる。たとえば自宅 PC で 100 ms だった処理が、研究室の計算サーバーでは 80 ms になったり 120 ms になったりする。1 回の計測からは、入力が変わったとき・マシンが変わったとき・言語を替えたときの性能をほとんど推測できない。

そこで公正な比較をできるように、RAM モデルというのを考えてその設定の中で計算時間を図るようにすればよいという話の流れだった。

具体的にどう測るのか？

🔵Important 計算時間の数え方

  1. 擬似コードの各行が何回実行されるかを数える
  2. 各行の「1 回あたりコスト」を掛けて足し合わせる
  3. 合計コスト＝実行時間として数式として表す
  4. ランタイム比較にとって本質的な項（たとえば最高次数項）だけを取り出す

こうすれば、実測に頼らずとも「入力が 2 倍になったら時間はどの程度増えるか」を予測できる。

実行時間は入力のインスタンスに依存する

挿入ソートをどう解析するか。まず実行時間が入力に依存することを認識する必要がある。入力には多くの特徴があるが、とくに、入力サイズ $n$ に着目してプログラムの実行時間を入力サイズの関数として表すのが一般的だ。

入力には多くの特徴がある書いたが、入力サイズに加えてどんな特徴があるだろう？挿入ソートに固有の入力に応じた性質でいうと具体的に以下のようなものがある。

🔘Note 挿入ソートの入力に応じた性質

  • 入力サイズ $n$ が大きいほど時間は増える
  • すでにほぼ整列されている配列なら高速に終わる
  • 完全に逆順の配列だと挿入回数が最大になり、最悪ケースを引き起こす

1000 個の数を並べ替える方が 3 個を並べ替えるより時間がかかるのは当たり前だが、さらに、同じサイズの 2 つの入力配列でも、既にどれだけ整列されているかによって挿入ソートの実行時間は変わるというのが面白い特徴だ。

たとえば、昇順に並べ替えるタスクをこなす挿入ソートに以下のような２つの入力配列を与えてみて実行回数のオーダーを比較しよう。こんな感じになるはずだ。

入力配列 実行の様子 実行回数のオーダー ケース
[1,2,3,4] ほぼ比較せずに次の要素へ進む $\Theta(n)$ 最良
[4,3,2,1] 各要素を先頭まで移動 $\Theta(n^2)$ 最悪

このように入力のインスタンスによって、最悪な例だったり最良な例だったりする。一般的にアルゴリズムの解析を行うときは以下の3つに分けて考える。

🔵Important どんなケースでアルゴリズムを解析しているのか

  • 最悪ケース解析 ：どんな入力を渡しても超えない上限を保証。アルゴリズムの堅牢性を測れる。
  • 最良ケース解析 ：あくまで参考値。チューニングの指針にはなるが、保証は弱い。
  • 平均ケース解析：入力分布を仮定するときに有用。たとえば乱数列を等確率で受け取る検索木など。詳しくは第５章乱択アルゴリズムで扱う。

挿入ソートの場合、最悪ケースが $\Theta(n^2)$、最良ケースが $\Theta(n)$ と大きく離れるためどちらのケースで解析したのか明瞭にしなければならないことがすぐにわかると思う。挿入ソートに限らず一般的にアルゴリズムを解析する場合、どのケースで解析しているのかを明確にする必要がある。

入力サイズをどのように定めるのか？

さて、話を戻して、このように入力の特徴は入力サイズのほかにもあるわけだが、基本的には入力サイズをもとに実行時間を測定することになる。

では、この入力サイズはどのように定めればよいのだろうか？

→　入力サイズの最適な指標は問題によって異なる。

たとえば、ソートや離散フーリエ変換のような問題では、入力要素数が最も自然な尺度であり、並べ替える要素数 $n$ がそれに当たる。

ほかにも、整数の乗算のような問題では、入力を 2 進表記したときに必要な 総ビット数 が適切な尺度となる。

あるいは、入力がグラフの場合には、頂点数と辺数の 2 つの値でサイズを表すのが普通だ。この本では扱う各問題について、どの入力サイズ尺度を用いるかをきちんと明示する。

実際に挿入ソートの計算時間を数えてみる（一般式）

挿入ソートの各行にコスト定数 $c_j$ を cost 、それぞれ何回その命令を実行するかを times として書くと以下のようになる。

INSERTION-SORT(A, n)              　cost    times

1  for i = 2 to n                 　c1      n
2      key = A[i]                 　c2      n − 1
3      // 部分配列 A[1:i-1] に挿入
4      j = i − 1                  　c4      n − 1
5      while j > 0 and A[j] > key 　c5      Σ_{i=2}^{n} t_i
6          A[j + 1] = A[j]        　c6      Σ_{i=2}^{n} (t_i − 1)
7          j = j − 1              　c7      Σ_{i=2}^{n} (t_i − 1)
8      A[j + 1] = key             　c8      n − 1

コスト定数 $c_j$ をかけ合わせてそれぞれ命令数分足し合わせると実行時間は、入力サイズ $n$ を用いて以下のような多項式の関数 $T(n)$ で表せる。

$$ \begin{aligned} T(n) &= c_{1}n + c_{2}(n-1) + c_{4}(n-1) \\ &\phantom{=} + c_{5}\sum_{i=2}^{n} t_i + c_{6}\sum_{i=2}^{n}(t_i-1) \\ &\phantom{=} + c_{7}\sum_{i=2}^{n}(t_i-1) + c_{8}(n-1) \end{aligned} $$

これは実行時間の一般式である。入力ケースに応じて、While ループがどれくらい繰り返すか変わる、すなわち $t_i$ の値が入力ケースに応じて変化する。以下では、最良ケースと最悪ケースの計算時間について検討する。

最良ケース

挿入ソートでは、配列がすでに昇順の場合が最良ケースである。この時の実行時間について考える。

この場合、行 5 が実行されるたびに key（元々 $A[i]$ に入っていた値）が $A[1:i−1]$ のすべての値以上 であるため、行 5–7 の while ループは行 5 の最初の判定で必ず終了する。したがって、

$$t_i = 1 \qquad (i = 2,3,\dots ,n)$$

となり、最良ケースの実行時間は

$$ \begin{aligned} T(n) &= c_1 n + c_2 (n-1) + c_4(n-1) + c_5(n-1) + c_8(n-1) \\ &= (c_1 + c_2 + c_4 + c_5 + c_8)n - (c_2 + c_4 + c_5 + c_8) \end{aligned} $$

ここで $$a=c_{1}+c_{2}+c_{4}+c_{5}+c_{8}$$ $$b=-(c_{2}+c_{4}+c_{5}+c_{8})$$ と置けば

$$ T(n)=an + b $$

となり、実行時間は 入力サイズ n に対して線形関数 である。

最悪ケース

最悪ケースは配列が完全な降順（逆順）で与えられるときに生じる。

このとき、手続きは各要素 $A[i]$ を 整列済み部分 $A[1:i−1]$ の全要素 と比較しなければならないので、

$$ t_i = i \qquad (i = 2,3,\dots ,n) $$

となる（行 5 で毎回 A[j] > key が真になり、while ループは j が 0 になるまで続く）。

次の等式を用いると

$$ \begin{aligned} \sum_{i=2}^{n} i = \Bigl(\sum_{i=1}^{n} i\Bigr) - 1 = \frac{n(n+1)}{2} - 1 \\ \sum_{i=2}^{n} (i-1) = \sum_{i=1}^{n-1} i = \frac{n(n-1)}{2} \end{aligned} $$

最悪ケースの実行時間は

$$ \begin{aligned} T(n) &= c_{1}n + c_{2}(n-1) + c_{4}(n-1) + c_{5}\Bigl(\frac{n(n+1)}{2} - 1\Bigr) + c_{6}\Bigl(\frac{n(n-1)}{2}\Bigr)\\ &\quad+ c_{7}\Bigl(\frac{n(n-1)}{2}\Bigr) + c_{8}(n-1)\\ &= \Bigl(\tfrac{c_{5}}{2} + \tfrac{c_{6}}{2} + \tfrac{c_{7}}{2}\Bigr)n^{2} + \Bigl(c_{1}+c_{2}+c_{4}+\tfrac{c_{5}}{2}-\tfrac{c_{6}}{2}-\tfrac{c_{7}}{2}+c_{8}\Bigr)n \\ &\quad- (c_{2}+c_{4}+c_{5}+c_{8}) \end{aligned} $$

ここで

$$ a = \frac{c_{5}}{2} + \frac{c_{6}}{2} + \frac{c_{7}}{2}, $$ $$ b = c_{1}+c_{2}+c_{4}+\frac{c_{5}}{2}-\frac{c_{6}}{2}-\frac{c_{7}}{2}+c_{8}, $$ $$ c = -(c_{2}+c_{4}+c_{5}+c_{8}) $$

と置くと

$$ T(n) = an^{2} + bn + c $$

となり、実行時間は 入力サイズ n に対して 2 次関数 である。

🔘Note アルゴリズムの解析まとめ

  • アルゴリズムの実行時間は「各文を実行するコスト × 回数」の総和
  • 擬似コード 1 行の実行には 定数時間 $c_k$ を仮定する（RAM モデル）
  • for や while が自然に終了するとき、ループ本体より 回数が 1 回多い
  • コメントは実行されないので コスト 0 とする
  • 入力サイズ $n$ の関数 $T(n)$ を求めれば，他の PC や実装でも傾向を予測できる。

増加のオーダー

挿入ソートのアルゴリズム解析を行うにあたって、最良ケースと最悪ケースの実行時間を以下のように簡略的に表した。

最良ケース 最悪ケース
$T(n)$ $an + b$ $an^{2} + bn + c$

さらに簡略化しよう。僕たちが本当に関心があるのは、実行時間の増加率つまり、増加のオーダーだ。したがって、式の中では先頭項（例えば $an^2$）のみを考慮し、低次の項は無視する。というのも、入力サイズ $n$ が大きくなると、低次の項は相対的に重要性が小さくなるからだ。

また、先頭項の定数係数も無視する。これは、入力が大きくなるほど、計算効率において重要なのは定数よりも増加率だからだ。すると以下の表のようになる。

最良ケース 最悪ケース
$n$ $n^{2}$

すごくシンプルだ。

例として、あるアルゴリズムが特定のマシンでサイズ $n$ の入力に対して $n² / 100 + 100n + 17$ マイクロ秒かかるとする。このとき、$n^2$ 項の係数（1/100）と $n$ 項の係数（100）では4桁の差があるが、$n$ が10,000を超えると $n^2 / 100$ 項の方が $100n$ 項を支配するようになる。10,000は一見大きく思えるが、平均的な町の人口より小さい。実際の問題では、さらに大きな入力サイズが普通にあり得る。

実行時間の成長のオーダーを強調するために、ギリシャ文字の「$\Theta$（シータ）」を使った特別な記法がある。それを使うと以下の表のように書ける。

最良ケース 最悪ケース
$\Theta(n)$ $\Theta(n^{2})$

今のところは、$\Theta$ 記法を「 $n$ が大きいときにおおよそ比例する」と理解しておけばよい。つまり、$\Theta(n^{2})$ は「$n^2$ に比例する」という意味だ。

厳密な定義については第３章で扱う。

練習問題

2.2-1

関数
$$\frac{n^3}{1000} + 100n^2 - 100n + 3$$ を $\Theta$ 記法で表現しなさい。

主要項は $\frac{n^3}{1000}$ なので、低次項と係数を無視して、$\Theta(n^3)$ .

2.2-2

配列 $A[1 : n]$ に格納された $n$ 個の数をソートすることを考える。まず、$A[1 : n]$ の中で最小の要素を見つけ、それを $A[1]$ と交換する。次に、$A[2 : n]$ の中で最小の要素を見つけ、それを $A[2]$ と交換する。さらに、$A[3 : n]$ の中で最小の要素を見つけ、それを $A[3]$ と交換する。この操作を、A の最初の $n - 1$ 個の要素に対して繰り返す。

(1) このアルゴリズム（選択ソート）の擬似コードを書きなさい。

(2) このアルゴリズムはどのようなループ不変式を維持しているか？

(3) なぜこのアルゴリズムは、すべての $n$ 個の要素ではなく、最初の $n - 1$ 個の要素だけに対して実行すれば十分なのか？

(4) 選択ソートの最悪ケース実行時間を $\Theta$ 記法で示しなさい。

(5) 最良ケース実行時間はそれより良くなるか？

(1) 疑似コード

SELECT-SORT(A,n)

i = 1
for i to n-1:
	min_j = i
	j = i+1                 // j=i でもよいがこちらのが無駄がない
	for j to n-1
		if A[j] < A[min_j]
			min_j = j
	swap(A[i], A[min_j])    // A[i] と A[min_j] を入れ替える

j=i+1 のところについて、 A[i] と比べても必ず < にはならないので、j=i ではなく、j=i+1 として1 回分ムダな比較を省いている。

(2) 外側ループが始まる時点で、配列の先頭 i−1 要素には入力中で最も小さい i−1 個の値が昇順で格納されている。

(3) 外側ループを $n−1$ 回繰り返せば、先頭 $n−1$ 要素がすでに最小から順に並んでいる。残る最後の 1 要素は 「未選択かつ唯一の要素」 であり、その値は配列中で最大（または降順なら最小）になる。したがって $n-1$ 回で位置は確定する。

(4) 最悪ケースの実行時間について、

  • 比較回数
    • 内側ループの長さは $(n−1) + (n−2) + … + 1$
    • 総和は $\frac{n(n−1)}{2} = \Theta(n^2)$
  • 交換回数は高々 $n−1 = \Theta(n)$
  • 比較コストが支配的なので最悪実行時間は $\Theta(n^2)$

(5) 最良ケースでも早くならない。なぜなら、選択ソートは配列の順番に関係なく毎回未整列部分全体を走査して最小値を探すから。比較回数は常に $\frac{n(n−1)}{2}$ で、入力がすでに整列済みでも省略できない。交換は 0 回で済むが、計算量オーダーは $\Theta(n^2)$ のまま。

参考： judge.u-aizu.ac.jp/onlinejudge/description.jsp?id=ALDS1_2_B&lang=ja

2.2-3

線形探索について再び考える（練習問題 2.1-4 を参照）。探索対象の要素が配列内のどの要素である可能性も等しいと仮定する。このとき、

(1) 平均して何個の要素をチェックする必要があるか？

(2) 最悪の場合はどうか？

(3) $\Theta$ 記法を使って、線形探索の平均ケースおよび最悪ケースの実行時間を示しなさい。

(4) 答えに対する理由付けも行いなさい。

(1) 平均してチェックする要素数

確率変数 $X = v$ を発見するまでに比較した要素数とおくと

$$\Pr[X=i]=\frac1n\quad(i=1,2,\dots ,n)$$ 期待値は $$\mathbb{E}[X]=\sum_{i=1}^{n} i\cdot\frac1n =\frac1n\cdot\frac{n(n+1)}2 =\frac{n+1}{2}$$ (2) 最悪の場合のチェック数

$v$ が末尾 $A[n]$ にある（あるいは存在しない）とき $n$ 個 すべてを調べる必要がある。

(3) 平均ケース・最悪ケースの実行時間

  • 平均ケース実行時間 $$T_{\text{avg}}(n)=Θ!\left(\frac{n+1}{2}\right)=Θ(n)$$
  • 最悪ケース実行時間 $$T_{\text{worst}}(n)=Θ(n)$$

(4) 理由付け

比較回数がそのままアルゴリズムの主要コストになる。

  1. 平均ケース
    • 位置が一様分布 → 比較回数の期待値が $(n+1)/2$
    • 定数倍を除き $n$ に比例するので $\Theta(n)$
  2. 最悪ケース
    • $v$ が最後に現れるか存在しない → すべて調べる。
    • 比較回数は常に $n$
    • したがって $\Theta(n)$

2.2-4

任意のソートアルゴリズムを、最良ケースの実行時間が良くなるように修正するには、どのようにすればよいか？

「入力がすでに整列済みかを最初に 1 回だけ線形時間でチェックし、そうであればそのまま返す」という早期終了処理を付け加える。

アルゴリズムの設計

どんな設計手法があるのか？

アルゴリズムの設計手法にはいろいろな選択肢がある。挿入ソートは「逐次添加法（Incremental Method）」に分類されるアルゴリズムで、以下の表でいうと３番に含まれている。

分類（代表例） 説明 典型アルゴリズム例
1. 全探索／力任せ（Brute-Force） 全ての候補を列挙して最良解を探す 文字列検索、部分集合和の全探索
2. 分割統治法（Divide & Conquer） 同型の部分問題に分割 → 再帰的に解き → 結果を合成 マージソート、クイックソート、ストラッセン行列積
3. 漸化式型／逐次添加型（Decrease & Conquer） 問題サイズを1ずつ減少（または増加）させながら解を構築 挿入ソート、二分探索、ユークリッド互除法
4. Transform & Conquer 入力を別表現に変換して解きやすくする ヒープソート（ヒープ化）、QR分解、AVL木の回転
5. 動的計画法（Dynamic Programming） 重複部分問題をメモ化して小→大の順で解く ナップサック、ワーシャル–フロイド、編集距離
6. 貪欲法（Greedy） 局所最適を積み重ね全体最適を目指す（最適性保証は問題依存） ダイクストラ、プリム／クラスカル、ハフマン符号化
7. バックトラック／分枝限定 解空間を深さ優先で探索し、不要枝を剪定 Nクイーン、数独、巡回セールスマンへの枝限定＋帰着
8. 乱択アルゴリズム（Randomized） 乱数に基づく手続きで期待性能を向上または簡潔化 ランダム化クイックソート、モンテカルロ積分
9. 近似・ヒューリスティクス NP困難問題に対し近似比や経験則で実用解を多項式時間で構築 2-approx TSP、局所探索／タブーサーチ、シミュレーテッドアニーリング
10. 並列・分散アルゴリズム マルチコア／クラスタで並行実行し通信コストも考慮 MapReduceフレームワーク、PRAMモデルアルゴリズム
11. 外部メモリ／キャッシュ意識型 I/O階層を意識し転送回数を最小化 B木、キャッシュオブリビアスマトリックス乗算
※ この表は、The Algorithm Design Manual の目次を参考にブログの筆者が作りました。

分割統治法

分割統治法を用いて、挿入ソートよりも最悪実行時間が大幅に短いソーティングアルゴリズムを設計する。分割統治法について詳しいことは第４章で扱う。ここでは、分割統治法により設計されたアルゴリズムの実行時間の解析が容易であることを感じられるとよい。

有用なアルゴリズムはしばしば再帰的な構造を持っている。再帰的とはなにか？

🔵Important 再帰的手続きとは

自己を一度または複数回呼び出して、部分問題を処理するような手続きのこと。

よくある再帰的な手続きとして、階乗の計算がある。以下のような感じ。

FACTORIAL(n)

if n == 0
	return 1
else
	return n × FACTORIAL(n-1)

階乗を求める手続きの中で、手続き自分自身を呼び出している。分割統治法はこのような再帰的な構造を持つ。

分割統治法においては、問題が十分小さい場合（基本ケース）には、再帰せず直接解を求める。それ以外の場合（再帰ケース）には、以下の三つの基本ステップを実行する。

🔘Note

  1. 分割 (Devide)：問題を、元の問題と同種だが規模が小さい1個以上の部分問題に分割する
  2. 統治 (Conquer)：それらの部分問題を再帰的に解決する
  3. 結合 (Combine)：部分問題の解を組み合わせて、元の問題の解を構成する

マージソートは分割統治法

マージソートアルゴリズムは、この分割統治法のやり方に従っているアルゴリズムだ。

各ステップでは部分配列 $A[p : r]$ をソートすることを目指し、最初は配列全体 $A[1 : n]$ を対象とし、より小さな部分配列へと再帰的に処理を進める。

マージソートの手順は次のとおりである。

  1. 分割：配列 $A[p:r]$ を中央のインデックス $q$ で 2 つに分ける
  2. 統治 (再帰呼び出し)：左半分 $A[p…q]$ と右半分 $A[q+1…r]$ をそれぞれソート
  3. 結合 (マージ)：2 つの整列済み部分配列を 1 つにまとめる

この再帰処理が「端っこまで来る」のは、ソート対象の部分配列が 要素 1 つ、すなわち p == r になったとき。要素が 1 つだけの配列は自明に整列済みなので、これ以上は処理を分割せず上の処理へ戻る。

マージソートにおける主要な操作は「結合（combine）」ステップであり、隣接する二つのソート済み部分配列を結合する。このマージ操作は補助手続き MERGE(A, p, q, r) によって実行される。

マージ操作をざっくり理解する

マージ操作ではどのようにして部分配列の結合を行っているのか見てみよう。

🔘Note マージ操作ざっくり説明

ここで、$A$ は配列、$p,q,r$ はその配列内のインデックスであり、$p \leq q < r$ を満たすと仮定する。

  • 一時配列 L, R を用意
    • L ← A[p:q]
    • R ← A[q+1:r]
  • 番兵（∞）を末尾に置く
    • 実装を簡潔にするため、L と R の末尾に非常に大きな番兵値を追加する
  • メインループ
    • L と R の 先頭要素 を比較し、小さい方を A[k] に書き戻す
    • 比較ごとにその配列のポインタを 1 進める
    • k をインクリメントして次の書き込み位置に移る
  • いずれかの配列が空になったら終了
    • 番兵のおかげで境界チェックはいらない

トランプでイメージするマージ操作

トランプで考えてみよう。机の上に 表向き に置いた 2 つの山がある。どちらも 昇順 に並んでいて山の一番上が最小値だ。

  1. 2 枚の「各山の一番上のカード」を見比べて、小さい方を取り出す
  2. それを 裏向き にして新しい 3 つ目の山（出力）に重ねる
  3. どちらかの山が空になるまで 1–2 を繰り返す
  4. 残った山全体を裏返して出力の山に載せれば完成する

要は、マージ操作とは単純に「先頭要素だけを比較」して結合する操作といえる。

マージ操作疑似コード

MERGE(A, p, q, r)

1   n_L = q - p + 1            // A[p:q] の長さ
2   n_R = r - q                // A[q+1:r] の長さ
3   let L[0:n_L −1] および R[0:n_R −1] を新規配列として確保
4   for i = 0 to n_L −1        // A[p:q] を L[0:n_L−1] にコピー
5       L[i] = A[p + i]
6   for j = 0 to n_R −1        // A[q+1:r] を R[0:n_R−1] にコピー
7       R[j] = A[q + j + 1]
8   i = 0                      // L の未マージ要素中の最小要素を指すインデックス
9   j = 0                      // R の未マージ要素中の最小要素を指すインデックス
10  k = p                      // A に書き戻す位置を指すインデックス
11  // L と R のどちらにも未マージ要素がある限り、
12  while i < n_L and j < n_R
13      if L[i] ≤ R[j]
14          A[k] = L[i]
15          i = i + 1
16      else
17          A[k] = R[j]
18          j = j + 1
19      k = k + 1
20  // 一方の配列を使い切ったら、もう一方の残りを A[p:r] の末尾にコピー
21  while i < n_L
22      A[k] = L[i]
23      i = i + 1
24      k = k + 1
25  while j < n_R
26      A[k] = R[j]
27      j = j + 1
28      k = k + 1

マージソート疑似コード

MERGE-SORT(A, p, r)

1   if p ≥ r                 // 要素が 0 個または 1 個か？
2       return
3   q = ⌊(p + r) / 2⌋        // A[p:r] の中点を求める
4   MERGE-SORT(A, p, q)      // 再帰的に A[p:q] をソート
5   MERGE-SORT(A, q + 1, r)  // 再帰的に A[q+1:r] をソート
6   // A[p:q] と A[q+1:r] を A[p:r] にマージ
7   MERGE(A, p, q, r)

サブルーチンとして MERGE を呼び出して再帰的な処理をしている。

ここで、3行目にフロア関数を用いているので、フロア関数の定義を載せておく。

🔘Note フロア関数 (床関数)

$$\lfloor x \rfloor := \max { n \in \mathbb{Z} \mid n \leq x }$$

大学入試ではガウス記号 $[x]$ としてあらわしてたやつです。

マージソート具体例

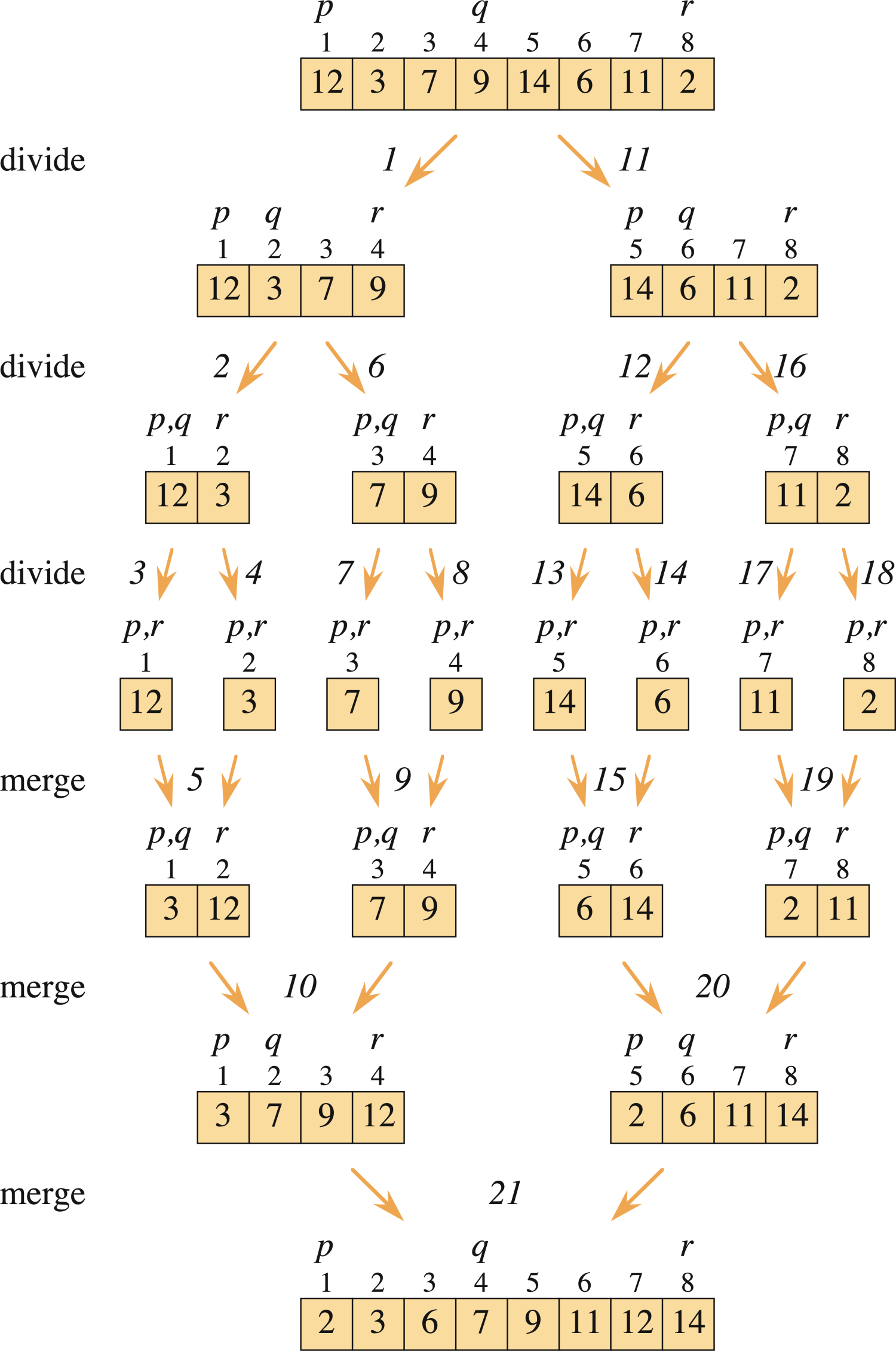
Figure2_4.png

出典：『Introduction to Algorithms 4th Edition』Figure2.4

【参考になるマージソートの動画 1】

【参考になるマージソートの動画 2】

分割統治法の解析

再帰呼び出しが含まれるアルゴリズムを解析する場合、漸化式を立てて考える。漸化式を解くことで、アルゴリズムの性能に関する上界や下界などを数学的に求めることができる。

分割統治アルゴリズムはおおむね 「分割 → 各部分を解く → 統合」 の三段階で動く。次の変数を置くと、最悪時間 $T(n)$ は

記号 意味
$a$ 生じる部分問題の個数
$b$ 各部分問題のサイズの縮小率（もとの $1/b$）
$D(n)$ 問題を分割するのに要する時間
$C(n)$ 部分解を統合するのに要する時間

となり、漸化式は

$$T(n)= \begin{cases} \Theta(1) & (n < n_0) \\ D(n)+a T\left(\tfrac{n}{b}\right)+C(n) & (n \ge n_0) \end{cases}$$

となる。

マージソートでは $a=2,b=2$ だが、ほかの分割統治法のアルゴリズムでは $a\neq b$ のこともある。

🔘Note 補足

$n_0$ は「これ以上小さい入力なら単純な解法で十分」という閾値。実装では $16$ や $32$ あたりの定数を選び、挿入ソートに切り替えたりすればよいと思います。

分割で $n/b$ が整数にならなくても、たとえばマージソートは

$$\lceil n/2\rceil, \lfloor n/2\rfloor$$

に分けるだけで、大小差は高々 1 になる。

漸化式の漸近オーダー（$\Theta$ 記法）には影響しないので、解析では両方とも単純に $n/2$ とみなしてよい。

また、ほとんどの再帰アルゴリズムで

$$n < n_0 \Rightarrow T(n)=\Theta(1)$$

が成り立つため、論文や教科書ではベースケースを明示せず「$T(n)=D(n)+aT(n/b)+C(n)$」だけ書くことが多い。実装時は明示的に停止条件を入れる。

マージソートの解析

$T(n)$ を、$n$ 個の数に対するマージソートの最悪実行時間とする。この漸化式を次のように立てる。

  • 分割（Divide）
    • 配列の中央を計算するだけなので、定数時間で済む。よって、$D(n) = \Theta(1)$ である。
  • 統治（Conquer）
    • サイズ $n/2$ の部分問題を2つ再帰的に解くため、実行時間として $2T(n/2)$ を要する（切り上げ・切り捨てについては前述の通り無視する）。
  • 結合（Combine）
    • 長さ $n$ の配列をマージする操作は $\Theta(n)$ 時間かかるため、$C(n) = \Theta(n)$ である。

マージソートの解析において、$D(n)$ と $C(n)$ を加えると、$\Theta(n)$ と $\Theta(1)$ の和となり、これは $n$ に対して線形な関数である。すなわち、$n$ が十分に大きいとき、その実行時間は $n$ にほぼ比例する。

したがって、分割と結合をあわせた時間は $\Theta(n)$ であり、これを統治ステップの $2T(n/2)$ に加えると、マージソートの最悪実行時間に対する漸化式は次のようになる：

$$ T(n) = 2T(n/2) + \Theta(n) \tag{2.3} $$

第4章では マスター定理 が紹介されており、これにより $T(n) = \Theta(n \log n)$ であることが示される。

挿入ソートの最悪実行時間 $\Theta(n^2)$ と比較すると、マージソートは $n$ の因子を対数の因子 $\log n$ に置き換えた形となっている。

🔘Note マージソートいいね

対数関数はどの線形関数よりも成長が遅いため、マージソートのほうが挿入ソートより良い感じといえる。入力サイズ $n$ が十分大きくなると、$\Theta(n \log n)$ のマージソートは、$\Theta(n^2)$ の挿入ソートよりも高性能になる。

マージソート再帰木

ただし、マスター定理を使わずとも、漸化式 (2.3) の解が $T(n) = \Theta(n \log n)$ であることを直感的に理解することは可能である。簡単のため、$n$ を2の累乗とし、基本ケースを $n = 1$ と仮定する。すると、漸化式 (2.3) は以下のようになる：

$$ T(n) = \begin{cases} c_1 & \text{if } n = 1 \\ 2T(n/2) + c_2n & \text{if } n > 1 \end{cases} \tag{2.4} $$

ここで $c_1 > 0$ はサイズ1の問題を解く時間、$c_2 > 0$ は配列1要素あたりの分割・結合の時間である。

Figure2.5は、この漸化式 (2.4) の解法の1つとして「再帰木」を用いる方法を示している。

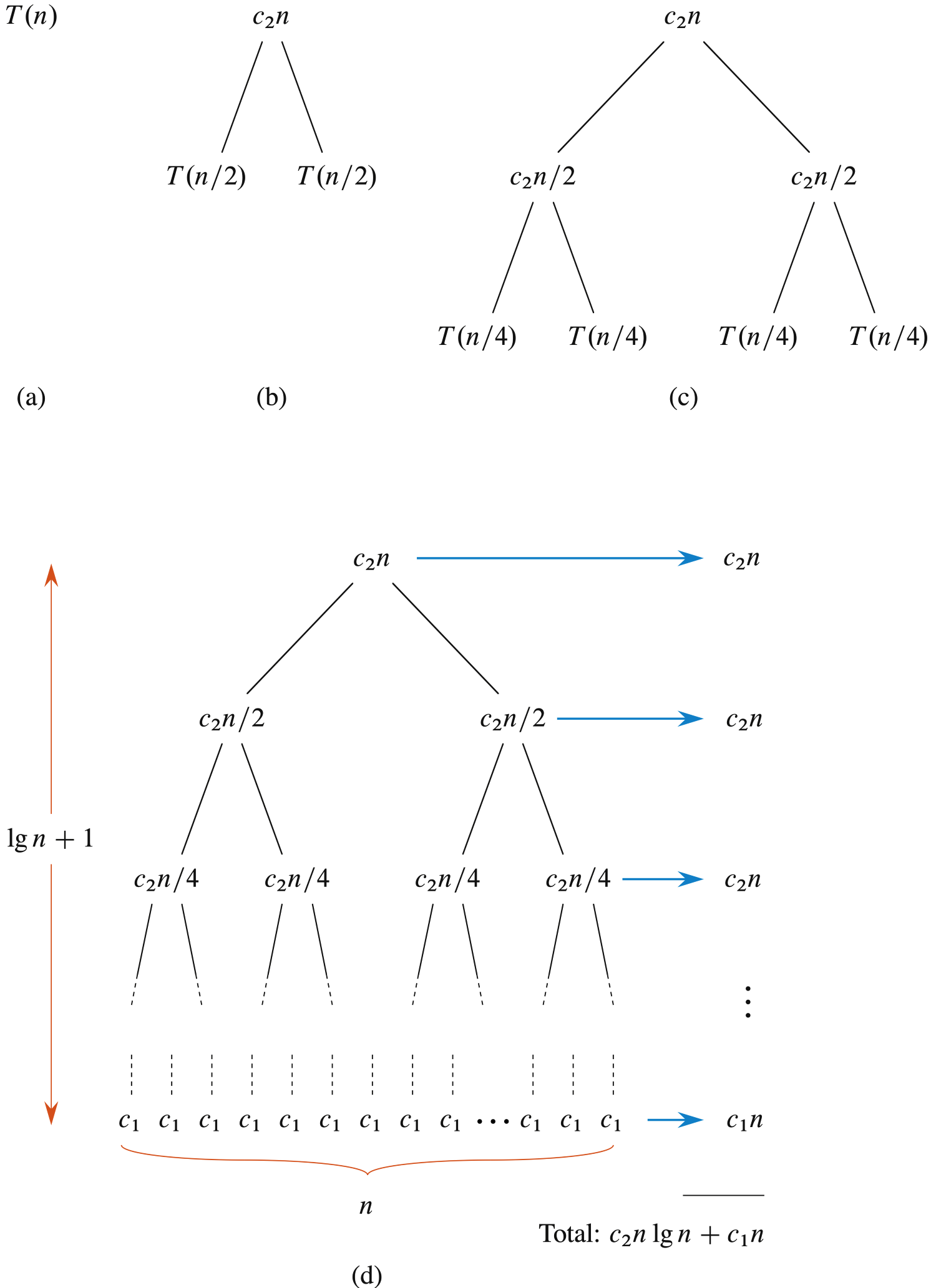
Figure2_5.png

出典：『Introduction to Algorithms 4th Edition』Figure2.5

  • 図(a)は $T(n)$ を示し、
  • 図(b)はそれを再帰木として展開したものである。最上位の分割・統合のコストが $c_2n$ であり、その左右の部分木が $T(n/2)$ に対応する。

次に、$T(n/2)$ をさらに展開して、図(c)では各部分が $T(n/4)$ に分割され、対応する各ノードの分割・統合コストが $c_2(n/2)$ となる。このようにして再帰木を下方に展開していき、問題サイズが1に達すると、各葉ノードのコストは $c_1$ になる。図(d)がその結果である。

次に、各レベルにおけるコストを合計する。

  • 最上位レベルのコストは $c_2n$
  • 次のレベルは $c_2(n/2) + c_2(n/2) = c_2n$
  • その次は $4 \times c_2(n/4) = c_2n$

というように、各レベルのノード数が2倍になる一方で、各ノードのコストは1/2になるため、レベルごとの合計コストは常に $c_2n$ で一定となる。

一般に、上から $i$ 番目のレベルでは、$2^i$ 個のノードがあり、それぞれのコストは $c_2(n / 2^i)$ であるから、合計コストは：

$$ 2^i \cdot c_2 \cdot \left(\frac{n}{2^i}\right) = c_2n $$

最下層には $n$ 個の葉ノードがあり、各ノードが $c_1$ のコストを持つため、合計で $c_1n$ となる。

再帰木のレベル数は $\log n + 1$ である（ここで $n$ は葉ノード数）。このことは帰納法で示すことができる。基本ケースでは $n = 1$ でレベル数は1、$\log 1 + 1 = 1$ で一致している。次に、葉ノードが $2^i$ 個のとき、レベル数は $\log 2^i + 1 = i + 1$ であり、次のサイズ $2^{i+1}$ に対してはさらに1レベル追加されて $i+2 = \log 2^{i+1} + 1$ となる。

よって、再帰木の総コストは、$\log n$ 個のレベルでそれぞれ $c_2n$ のコスト、最下層で $c_1n$ のコストを持つため、合計は：

$$ c_2n \log n + c_1n = \Theta(n \log n) $$

WIP : 時間あるときに解いたら回答を追記していきます。

練習問題

2.3-1

図2.4を参考にして、初期状態が配列 $\langle 3, 41, 52, 26, 38, 57, 9, 49 \rangle$ のとき、マージソートの動作を図示せよ。

2.3-2

MERGE-SORT 手続きの1行目にあるテストは if p \leq r ではなく if p \ne r となっている。もし p > r の状態で MERGE-SORT が呼ばれた場合、部分配列 $A[p : r]$ は空になる。初期呼び出しが MERGE-SORT(A, 1, n) であり、$n \geq 1$ のときは、if $p \ne r$ のテストで十分に p > r という再帰呼び出しを防げることを示せ。

2.3-3

MERGE 手続きの 12～18 行目の while ループに対するループ不変式を述べよ。また、それを使って 20～23 行目と 24～27 行目の while ループと併せて、MERGE 手続きが正しいことを示せ。

2.3-4

$n \geq 2$ が $2$ の累乗であるとき、以下の漸化式の解が $T(n) = n \log n$ であることを数学的帰納法を使って示せ。 $$ T(n) = \begin{cases} 2 & \text{if } n = 2 \\ 2T(n/2) + n & \text{if } n > 2 \end{cases} $$

2.3-5

挿入ソートを再帰アルゴリズムとして考えることもできる。$A[1 : n]$ をソートするには、まず $A[1 : n - 1]$ を再帰的にソートし、次に $A[n]$ をソート済み部分配列 $A[1 : n - 1]$ に挿入する。この再帰的バージョンの挿入ソートの疑似コードを記述せよ。その最悪実行時間に対する漸化式も与えよ。

2.3-6

探索問題（練習問題 2.1-4 を参照）に戻る。もし探索対象の部分配列がすでにソートされているならば、探索アルゴリズムはその中央の値を $v$ と比較して、配列の半分を探索対象から除外できる。二分探索アルゴリズム（binary search） はこの処理を繰り返し、残りの部分配列のサイズを毎回半分にしていく。このアルゴリズムの疑似コード（反復または再帰）を記述せよ。また、その最悪実行時間が $\Theta(\log n)$ であることを示せ。

2.3-7

セクション 2.1 にある INSERTION-SORT 手続きの 5～7 行目の while ループは、ソート済み部分配列 $A[1 : j - 1]$ に対して線形探索を行っている。もしこの線形探索の代わりに、練習問題 2.3-6 の二分探索を用いたとしたら、挿入ソートの最悪実行時間は $\Theta(n \log n)$ に改善されるだろうか？

2.3-8

整数の集合 $S$（サイズは $n$）と、別の整数 $x$ が与えられたときに、$S$ の中に合計がちょうど $x$ になる2つの要素が存在するかどうかを判定するアルゴリズムを記述せよ。そのアルゴリズムは最悪でも $\Theta(n \log n)$ 時間で動作すること。

章末問題

2-1 小さい配列に対するマージソートでの挿入ソートの利用

マージソートの最悪実行時間は $\Theta(n \log n)$、挿入ソートは $\Theta(n^2)$ であるが、挿入ソートの定数項が小さいため、実際の計算機では問題サイズが小さいときに挿入ソートの方が高速なことがある。このため、マージソートの再帰の葉を粗くして、部分問題が十分小さくなったときには挿入ソートを使うという変更は理にかなっている。以下を考える。長さ $n$ の配列を、長さ $k$ の $n/k$ 個の部分配列に分け、それぞれを挿入ソートでソートし、その後マージソートの方法で統合する。ただし、$k$ は適切に選ぶものとする。

a. 長さ $k$ の $n/k$ 個の部分配列を挿入ソートでソートするのに、最悪でも $\Theta(nk)$ 時間で済むことを示せ。

b. これらの部分配列をマージするのに、最悪でも $\Theta(n \log(n/k))$ 時間で済むことを示せ。

c. この修正済みアルゴリズムが最悪で $\Theta(nk + n \log(n/k))$ 時間で動作するとき、通常のマージソートと同じ計算量となるような最大の $k$ は $\Theta$ 記法でどう表せるか？

d. 実際には $k$ をどのように選ぶべきか？

2-2 バブルソートの正しさ

バブルソートは広く知られているが非効率なソートアルゴリズムである。隣接する要素を比較し、順序が逆ならば交換する操作を繰り返す。

BUBBLESORT(A, n)
1 for i = 1 to n - 1
2   for j = n downto i + 1
3     if A[j] < A[j - 1]
4       交換 A[j] と A[j - 1]

a. ソート後の配列を $A’$ とする。BUBBLESORT が正しいことを証明するには、終了することと以下を示す必要がある： $$A’[1] \leq A’[2] \leq \dots \leq A’[n] \tag{2.5}$$ この不等式を示すためには、他に何を証明する必要があるか？

b. 行 2〜4 の for ループに対する正確なループ不変式を述べ、それが成り立つことを証明せよ。この証明には本章で示されたループ不変式の構造を用いること。

c. (b) の終了条件を使い、行 1〜4 の for ループに対するループ不変式を述べ、不等式 (2.5) を証明せよ。こちらも本章でのループ不変式の構造に従って証明すること。

d. バブルソートの最悪実行時間は？ 挿入ソートの最悪実行時間と比べてどうか？

2-3 ホーナー法の正しさ

次数 $n$ の多項式 $$P(x) = \sum_{k=0}^{n} a_k x^k = a_0 + a_1x + a_2x^2 + \dots + a_nx^n$$ を、ある値 $x$ に対して評価したいとする。ホーナー法（Horner’s Rule） では、上記の多項式を以下のように括弧付きで再構成し、項の計算回数を減らす： $$P(x) = a_0 + x(a_1 + x(a_2 + \dots + x(a_{n-1} + x a_n)\dots))$$ この評価方法は繰り返し構造を持つため、次のようなアルゴリズム（疑似コード）で実装できる：

HORNER(A, n, x)
1 p = 0
2 for i = n downto 0
3     p = A[i] + x * p
4 return p

a. この手続きの実行時間は $\Theta$ 記法でどう表せるか？

b. 多項式の各項を 1 から計算する素朴な評価アルゴリズムの疑似コードを記述せよ。その実行時間は？ HORNER と比較せよ。

c. 次のループ不変式を考える： 行 2 のループの各反復の開始時点で、 $$p = \sum_{k=0}^{n - (i + 1)} A[k + i + 1] \cdot x^kp=k=0∑n−(i+1)​A[k+i+1]⋅xk$$ 項が存在しないときの総和は 0 と定義する。このループ不変式を用いて、終了時に $p = \sum_{k=0}^n A[k] \cdot x^k$ であることを示せ。

2-4 反転（Inversions）

配列 $A[1 : n]$ が $n$ 個の異なる数から成るとする。$i < j$ かつ $A[i] > A[j]$ のとき、ペア $(i, j)$ を 反転（inversion） と呼ぶ。

a. 配列 $\langle 2, 3, 8, 6, 1 \rangle$ の反転をすべて列挙せよ（5個ある）。

b. 集合 ${1, 2, \dots, n}$ の要素からなる配列のうち、最も多くの反転を持つものはどれか？その反転数はいくつか？

c. 挿入ソートの実行時間と、入力配列中の反転の数との関係は？理由も述べよ。

d. 任意の $n$ 要素の順列に対して、反転の数を最悪でも $\Theta(n \log n)$ 時間で求めるアルゴリズムを与えよ。（ヒント：マージソートを改良せよ）