15.1 活動選択問題(区間スケジューリング問題)
1つの会議室がある。会議室では同時に違うミーティングを行うことはできない。この会議室の利用を申請する $n$ 個のミーティングがある。ミーティング時間が被らないという前提のもとで、なるべく多くのミーティングを実施したい。
これを「活動選択問題」という最適化問題として定式化しよう。
同時には1つの活動しか利用できない資源の使用許可を申請する $n$ 個の「活動」の集合
を考える。各活動 $i$ には「開始時刻」 $s_i$ と「終了時刻」 $f_i$ がある。$0\le s_i
すなわち、$s_i\ge f_j$ または $s_j \ge f_i$ ならば $a_i$ と $a_j$ は両立可能である。
活動選択問題では、互いに両立可能な活動から構成される集合で、サイズが最大のものを求めることが目的である。これらの活動は、すでに終了時刻に関して昇順:
でソートされていることを仮定する。
それでは具体的な活動の集合を考えよう。両立可能な活動の集合はどう書けるか?
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| s_i | 1 | 3 | 0 | 5 | 3 | 5 | 6 | 7 | 8 | 2 | 12 |
| f_i | 4 | 5 | 6 | 7 | 9 | 9 | 10 | 11 | 12 | 14 | 16 |
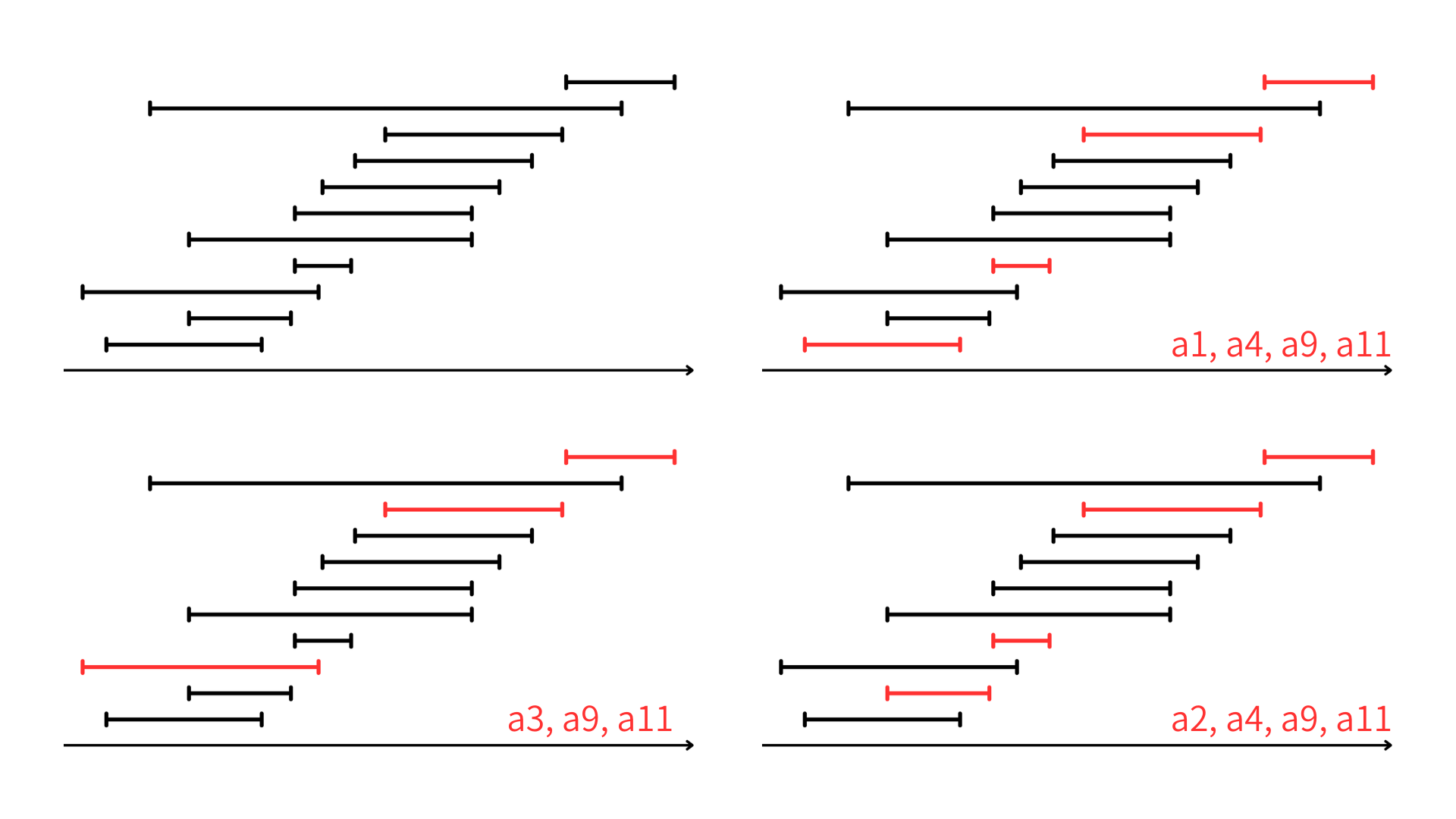
たとえば、部分集合 $\{a_3,a_9,a_{11}\}$ は互いに両立可能な活動から構成されている。これはサイズ最大の両立可能な活動の集合だろうか?
➡違う。なぜなら、$\{a_1, a_4, a_9, a_{11}\}$ も両立可能な活動から構成されており、こっちのほうがサイズが大きいからだ。そしてこれはサイズが最大の部分集合である。しかし、唯一というわけではなく、たとえば $\{a_2, a_4, a_9, a_{11}\}$ もサイズ最大の両立可能な活動の集合である。
表で見るとわかりにくいが、こんな風に図示すると両立してるかどうかは一目瞭然。
 この問題を解くために、いくつかのステップを踏む。
この問題を解くために、いくつかのステップを踏む。
- 動画計画法に基づく解法を考える
- 実はたった1つの選択(貪欲な選択)だけを考えればよいことに気づく
- そのためにはたった1つの部分問題だけが残る
- 再帰型の貪欲アルゴリズムを設計する
- 再帰を繰り返し型に変換する
➡アルゴリズム完成!
活動選択問題の最適部分構造
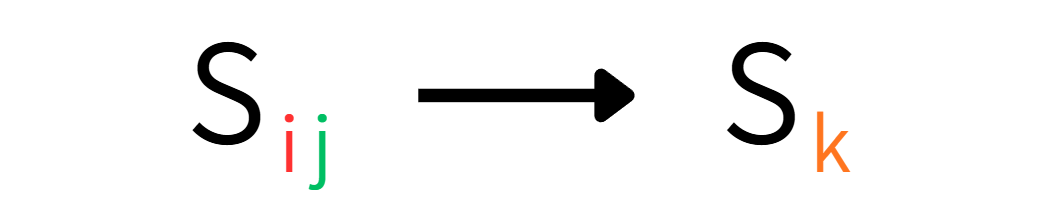
活動選択問題がまず最適部分構造を持つことを確かめる。活動 $a_i$ の終了後に開始し、活動 $a_j$ の開始前に終了する活動の集合を $S_{ij}$ とする。
たとえば、さっきの例で $S_{2,11}$ というと、以下のようになり、$S_{2,11}=\{a_4,a_6,a_7,a_8,a_9\}$ となる。
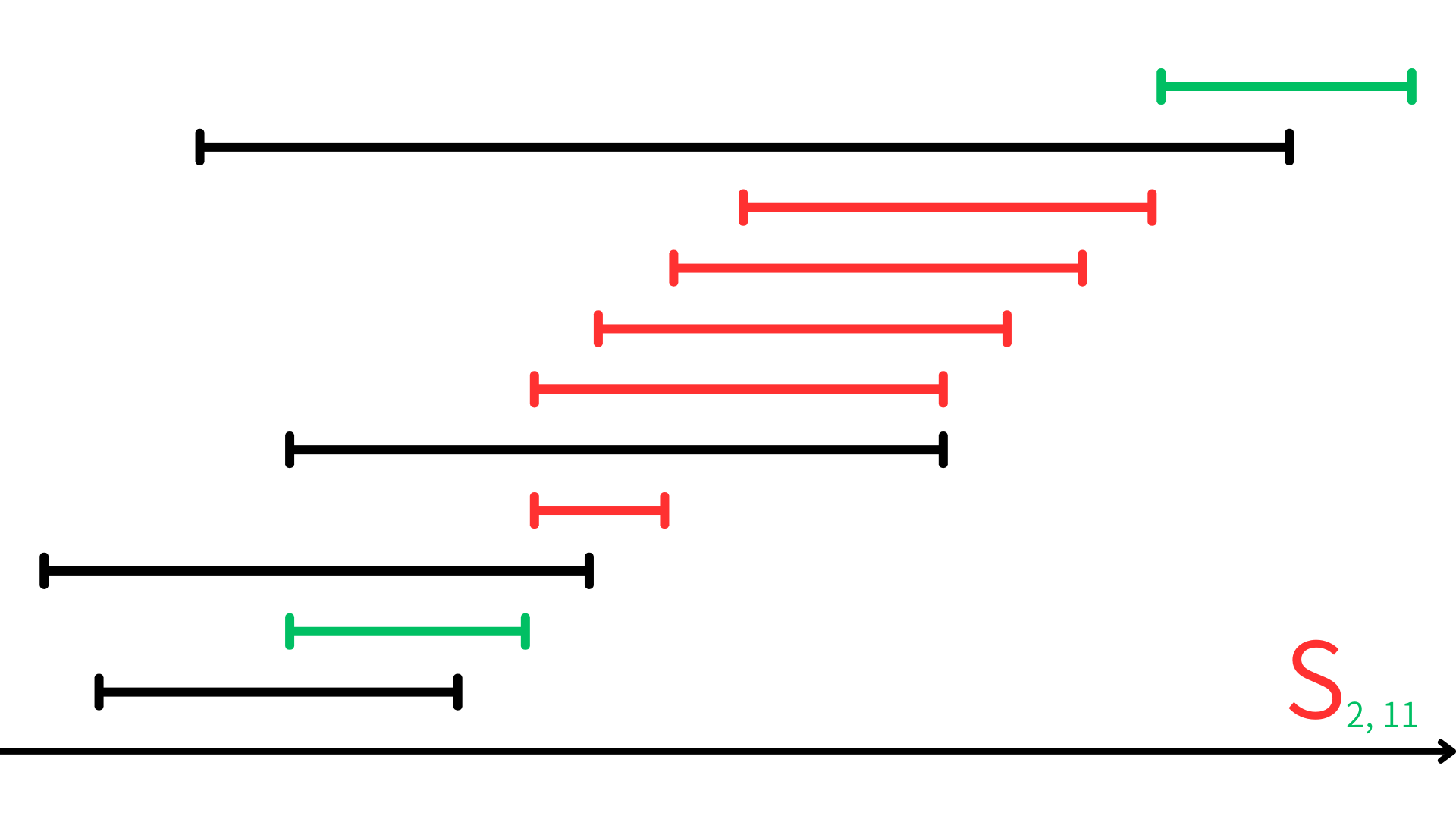
活動選択問題は言い換えると、$S_{ij}$ に属する互いに両立可能な活動から構成される集合の中で、サイズが最大のものを求める問題といえる。
さっきの例でいうと、$S_{0,12}$ に属する互いに両立可能な活動から構成される集合の中で、サイズがが最大のものを求める問題といえる。
$A_{ij}$ がその解の1つであり、ある活動 $a_k$ をその要素として含むと仮定しよう。$a_k$ を最適解に含めることによって、2つの部分問題に分けることができる。
つまり、$S_{ik}$ の中から互いに両立可能な活動を探す問題と、$S_{kj}$ の中から互いに両立可能な活動を発見する問題に分けることができる。
$A_{ik}$ と$A_{kj}$ は以下のように定義する:
- $A_{ik}=A_{ij}\cap S_{ik}$
- $A_{kj}=A_{ij}\cap S_{kj}$
つまり、$A_{ij}=A_{ik}\cup\{a_k\}\cup A_{kj}$ であり、$S_{ij}$ に属する互いに両立可能な活動から構成されるサイズが最大の集合である $A_{ij}$ は $|A_{ij}|=|A_{ik}|+|A_{kj}|+1$ 個の活動を含む。
最適解 $A_{ij}$ が $S_{ik}$ と $S_{kj}$ に対する部分問題の最適解を含む
【証明】
動的計画法のときによく使った「切り貼り論法」を使って証明する。
個の互いに両立可能な活動の集合化構成できるので、$A_{ij}$ の最適性に矛盾する。$S_{ik}$ に属する活動についても同様の議論が成立する。■
さあ、このように最適部分構造を見つけたので、動的計画法のお決まりのパターンに乗って漸化式を作ろう。
と書ける。さきほどは、$S_{ij}$ に対する最適解となる集合が $a_k$ を含むということを仮定して考えていたが、この仮定を取り払って考えると、$S_{ij}$ に属するすべての活動を $a_k$ の候補として調べる必要がある。したがって、
という漸化式を得る。
漸化式ができたので、これでトップダウンでもボトムアップでもどっちでもいいが動的計画法アルゴリズムを作れる。
貪欲な選択を行う
漸化式(15.2)に現れるすべての部分問題を解かなくてもいいとしたらどうだろう?それで最適解にたどり着けるならそっちのがいい。
実は、活動選択問題ではたった1つの選択「貪欲な選択」だけを考えればよい。
さて、この問題における「貪欲な選択」とは何だろうか?
a. 予定時間 (終了時刻 - 開始時刻の値) が短い予定を優先的に選んでいく b. 開始時刻が早い予定を優先的に選んでいく c. その予定と被っている予定の個数が少ない予定を優先的に選んでいく
どれもそれなりに良さそうに見える。しかし、上記のどの作戦も最適とはならないケースがある。
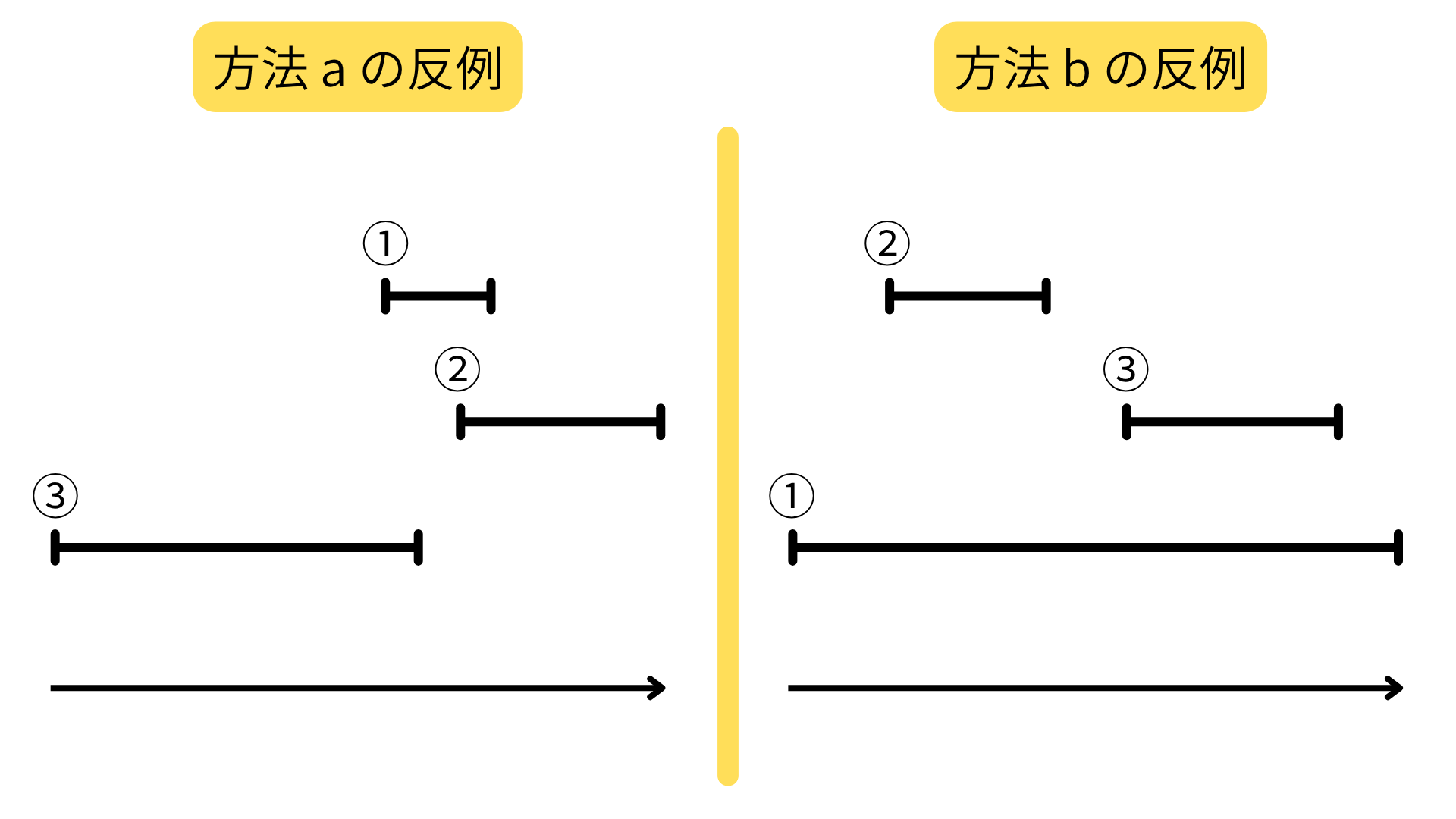
c については、同じ被り数の予定に対して、どのように順序付けるのか?という問題が残される。ここを任意にすると、ダメなパターンがある。
では、どういう方針で考えればよいか?
↓ ↓ ↓ ↓
➡ 直観的には、「できるだけ多くの活動が利用できる資源を後に残すように」すれば良さそう。つまり、「$S$ の中の終了時刻最小の活動を選択すべき」。これがこの問題の「貪欲選択」だ。
この貪欲選択を行うと、唯一の部分問題として、$a_1$ の終了後に開始する活動の集合から互いに両立可能な活動を見つける問題だけが残る。
終了時刻の昇順にソート済みであると式(15.1)で仮定したので、$a_1$ の開始前に終了する活動の集合を考える必要はない。なぜなら、$f_1$ は最小の終了時刻だから。
$S_k=\{a_i\in S :s_i\ge f_k\}$ を活動 $a_k$ の終了後の開始する活動の集合とする。活動 $a_1$ を貪欲選択すると、解くべき唯一の部分問題として $S_1$ が残る。最適部分構造によって、$S$ に対する最適解が $a_1$ を含むなら、それは $a_1$ と部分問題 $S_1$ に対する最適解に属するすべての活動から構成されることが分かる。
次に考えるべき大きな問題は「僕たちの直観は正しいのか?」ということ。つまり、この貪欲選択で最適解を導けるのか?ということ。
ではそれについて考えてみよう。
任意の空ではない部分問題 $S_k$ を考える。$a_m$ を $S_k$ に属する終了時刻最小の活動とする。このとき、$S_k$ に属する互いに両立可能な活動からなるサイズが最大の集合の中に $a_m$ を含むものがある。
【証明】
- $A_k$ を $S_k$ に属する互いに両立可能な活動から構成されるサイズが最大の集合
- $a_j$ を $A_k$ に属する終了時刻最小の活動
とする。
(1) $a_j=a_m$ のとき、
$a_m$ を含む $S_k$ に属する互いに両立可能な活動から構成されるサイズが最大の集合が存在し、定理は示された。
(2) $a_j\ne a_m$ のとき、
$A_{k}^{'}=(A_k -\{a_j\})\cup \{a_m\}$ を $A_k$ の $a_j$ を $a_m$ と交換したものとする。$A_k$ は互いに両立可能な活動の集合であり、$a_j$ は $A_k$ の中で最も早く終了し、$f_m\le f_j$ なので、$A_{k}^{'}$ もまた互いに両立可能な活動の集合である。
$|A_k^{'}|=|A_k|$ なので、$A^{'}_k$ は $a_m$ を含む $S_k$ に属する互いに両立可能な活動から構成されるサイズが最大の集合である。■
とりあえずここまでの話を整理する。
活動選択問題は動的計画法でも解けるが、「終了時刻最小の活動を貪欲に選択する」貪欲アルゴリズムできちんと最適解にたどり着ける。
貪欲アルゴリズムはトップダウン的な設計をする。活動を選択してから部分問題を解くのである。
再帰型貪欲アルゴリズム
ざっくりとした方針ができたので、具体的に再帰アルゴリズムを書いてみよう。
RECURSIVE-ACTIVITY-SELECTOR(s, f, k, n)
1. m = k + 1
2. while m =< n and s[m] < f[k] // S_k の中から終了時刻最小の活動を見つける
3. m = m + 1
4. if m =< n
5. return {a_m} ⋃ RECURSIVE-ACTIVITY-SELECTOR(s, f, m, n)
6. else return 空集合
活動が終了時刻に関してソート済みであると仮定すると、手続き RECURSIVE-ACTIVITY-SELECTOR(s, f, 0, n) の実行時間は $\Theta(n)$ である。なぜなら、すべての再帰呼び出しの全体を通して、各活動はちょうど1回だけ第2行の while ループの検査を受けることになるからだ。
このアルゴリズムの挙動を具体的なインスタンスを使って考えてみよう。最初に取り上げた、
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| s_i | 1 | 3 | 0 | 5 | 3 | 5 | 6 | 7 | 8 | 2 | 12 |
| f_i | 4 | 5 | 6 | 7 | 9 | 9 | 10 | 11 | 12 | 14 | 16 |
これに対して実行してみよう。すると以下の図のようになる。
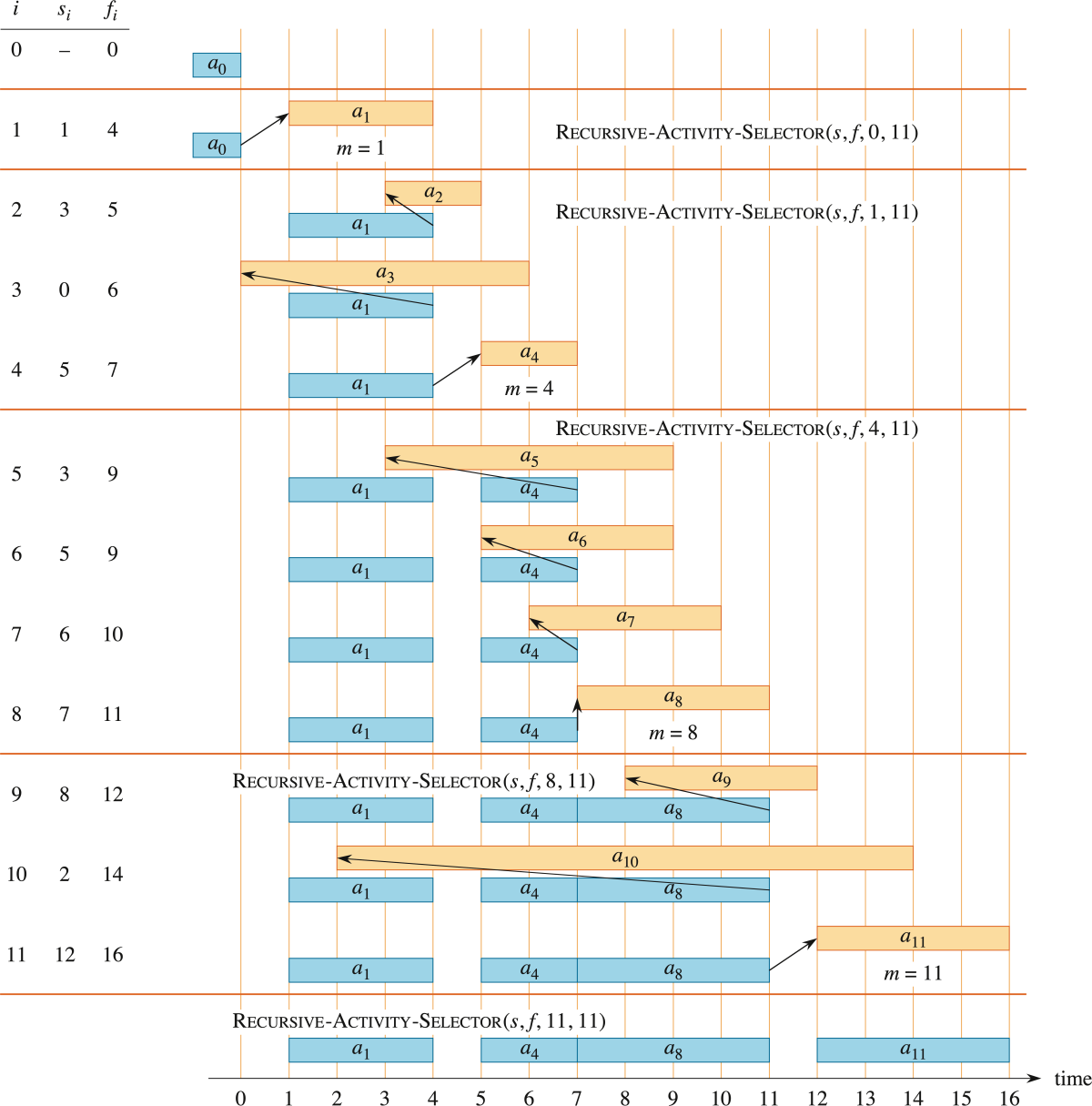
繰り返し型貪欲アルゴリズム
この再帰型アルゴリズムは簡単に繰り返し型に変換できる。というのも、これは「末尾再帰的」であって、自分自身に対する再帰呼び出しの後で集合和演算をおこなって終了するからだ。
末尾再帰(まつびさいき)とは、再帰的な手続きにおいて、自身の再帰呼び出しが、その計算における最後のステップになっているような再帰のパターンのことである。
今回でいえば最後に集合和演算を行っているだけで、自身の再帰呼び出しが最後のステップになっているのに近いので「末尾再帰的」と言っている。
繰り返し型アルゴリズムとして書き直すと以下のようになる。
GREEDY-ACTIVITY-SELECTOR(s, f, n)
1. A = {a_1}
2. k = 1
3. for m = 2 to n
4. if s[m] >= f[k] // a_m は S_k の要素か?
5. A = A ⋃ {a_m} // true なのでそれを選ぶ
6. k = m // そしてそこから継続する
7. return A
である。
このアルゴリズムも、再帰型と同様に、入力時に活動がその終了時刻の昇順でソート済みとすると、$n$ 個の活動からなる集合を $\Theta(n)$ 時間で解く。
15.2 貪欲戦略の要素
15.1 節では以下のような詳細すぎるステップを追って貪欲アルゴリズムを作った。
- 最適部分構造の特定
- 漸化式の導出
- 貪欲な選択で部分問題が1つに絞られることを示す
- 貪欲な選択で最適解へ到達できることを示す
- この貪欲選択を実装する再帰型アルゴリズムを作る
- 再帰型アルゴリズムをもとに繰り返し型アルゴリズムを作る
活動選択問題の場合は、ともに変化する2つの変数 $i,j$ を引数とする部分問題 $S_{ij}$ をまずステップ1,2で定義した。その後ステップ3で、常に貪欲な選択を行えば、$S_k$ という形に部分問題を減らせることを見出した。
別の方法として貪欲アルゴリズムの設計手順をまとめると以下のようになる。
- 対象となる最適化問題を、ある選択を行うと、その結果として解かなければならない1つの部分問題が残る問題とみなす
- 元の問題に対して貪欲な選択を行う最適解がつねに存在すること、したがって貪欲な選択はつねに「安全」であることを証明する
- 次のことを示すことで、最適部分構造を示す。つまり、貪欲な選択を行った後、残されたものは1つの部分問題で、その部分問題の最適解をあなたが行った貪欲な選択と合わせると、元の問題への最適解へ到達する、ということである。
貪欲選択性
どの貪欲アルゴリズムの背後にも、より複雑な動的計画法に基づく解法が存在する。
どのようにすれば与えられた最適化問題を貪欲アルゴリズムによって解けるか否かを判断できるだろうか?
➡ 常に適用可能な方法はない。しかし、2つのキーワードがある。
- 貪欲選択性
- 最適部分構造
である。与えられた問題がこの2つの性質を持つことを示せるならば、貪欲アルゴリズムの開発が順調に進むと考えてよい。
貪欲選択性とは、局所最適な(貪欲な)選択から大域最適な解を構成できるという性質のこと。
これは言い換えると、どれを選択するかを考えるときに、部分問題群から返される結果を考えずに、現段階の問題にとって最適に見える選択を行ってもよい、ということだ。
ここが貪欲アルゴリズムと動的計画法との違いである。
動的計画法でも各段階で選択を行うが、その選択は部分問題の解に依存する。結果として典型的には動的計画法をボトムアップ的に、小さい部分問題から解いていって大きい部分問題へと向かのである。
貪欲アルゴリズムによる選択は、過去の選択に依存するかもしれないが、未来の選択にも部分問題の解にも依存できない。
最初の選択を行う前にすべての部分問題を解く動的計画法と異なり、貪欲戦略は最初の選択を任意の部分問題を解く前に行う。
- 動的計画法:ボトムアップ的
- 貪欲アルゴリズム:トップダウン的
もちろん、貪欲な選択が大域的な最適解にたどり着くことを証明しなければならない。定理15.1 を見るとわかる通り、ある部分問題に対して大域的な最適解をまず調べる。次にこの大域的最適解を変形して、そこで用いたあるほかの選択を貪欲選択で置き換え、その結果、似てはいるがより小さい部分問題に帰着する方法を示すことで証明を行う。
貪欲アルゴリズムは動的計画法よりも効率よく実行できる。たとえば、活動選択問題では、入力される活動が終了時刻の昇順にソート済みなら各活動をちょうど1回検討するだけで済んだ。入力を前処理したり、適切なデータ構造を使えば、貪欲選択を高速化できて効率の良いアルゴリズムを設計できる。
最適部分構造
論証の仕方が貪欲アルゴリズムは、動的計画法と少し違う。
最適部分構造を貪欲アルゴリズムに適用するときには、元の問題に対して貪欲な選択を行うことで1個の部分問題が都合よく残されると仮定する。
あとは、この部分問題の最適解に、すでに行った貪欲な選択を組み合わせれば、元の問題に対する最適解が生成されることを論証するだけでよい。
これは、各ステップで行う貪欲な選択がつねに最適解を生成することを示すために、部分問題についての帰納法を裏で用いている。
貪欲法と動的計画法

動的計画法が使えるなら、すべて貪欲法が使えると誤解されることを避けるために、この2つの適用できる/できないについて微妙な違いのある以下の2つの問題を取り上げる。
- 0-1 ナップサック問題
- 有理ナップナック問題
泥棒が、重量 $W$ ポンドまで品物を運ぶことができるナップサックに、ある店の品物を入れて盗み出そうとしている。店にある $n$ 個の品物は、総重量が $W$ ポンド以内ならば、どの品物をナップサックに入れることができる。泥棒は盗む品物の総価値を最大化したいと思っている。$i$ 番目の品物は $v_i$ ドルの価値があり、重さは $w_i$ ポンドである。ただし、$v_i,w_i$ は自然数である。泥棒はどの品物をとるべきか?
この泥棒は、盗るか残すかの2択なので「0-1」と呼ばれている。部分的に盗んだり、同じものを複数回盗ることはできない。
0-1ナップサック問題とほとんど同様だが、泥棒は各品物に対して盗るか残すかの2択の判断ではなく、品物の一部を盗ることができるものとする。
イメージの違いとしては、「0-1」で扱う品物が「金の延べ棒」で、「有理」は「砂金」のようなものと思ってよい。
さて、この2つの問題は非常に類似しており、どちらも最適部分構造を持つが、片方は貪欲アルゴリズムで最適解にたどり着け、もう片方は貪欲アルゴリズムでは最適解にたどり着けない。
貪欲アルゴリズムで最適解にたどり着けるのはどっちだろうか?
↓ ↓ ↓ ↓
➡ 貪欲アルゴリズムで解けるのは「有理ナップサック問題」である。「0-1ナップサック問題は」貪欲アルゴリズムで解けない。
「有理」問題を解くには、各品物に対して1ポンド当たりの価値 $\displaystyle \frac{v_i}{w_i}$ を計算して、それが高い順にナップサックに運べるだけ詰めていけばよい。
品物をポンド当たりの価値でソートすることで、この貪欲アルゴリズムは $O(n\log n)$ 時間で動作する。
この貪欲戦略が「0-1」問題ではうまくいかないことを示す問題インスタンスが以下の図である。
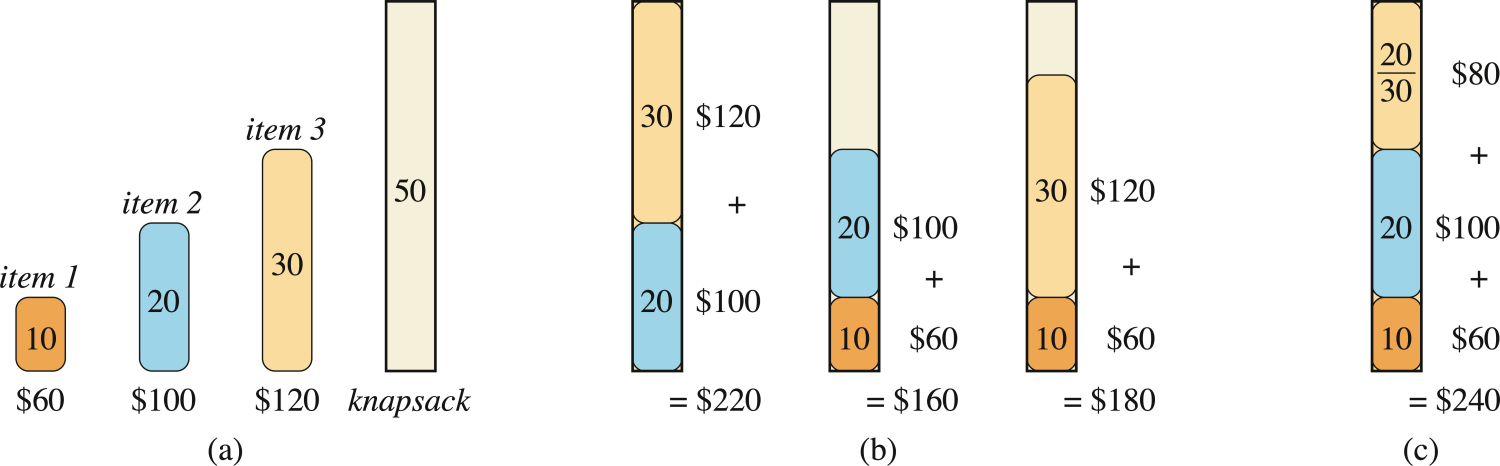
ポンド当たりの価値を計算すると、
- item1 : 60 / 10 = 6
- item2 : 100/ 20 = 5
- item3 : 120 / 30 = 4
item1 → item2 → item3 の順でバッグに入れていくことになるが、バッグの容量は50なので、item1とitem2だけ入る。このとき価値は160ドルだが、最適解は、item3とitem2を詰めて、総価値220ドルにすることである。
0-1問題では、ナップサックにある品物を入れるかどうかを決定するとき、その品物を含めた場合の部分問題の解を、その品物を除外した場合の部分問題の解と比較しなければならない。
15.3 ハフマン符号(ハフマン符号化)
文字列をビット文字列に置き換えてデータ送信することを考えよう。
情報を表現するためにはいろいろな方法があるが、ここでは、各文字をそれぞれ異なるビット文字列(=符号語)で表現する「2進文字符号」を設計する問題を考える。
たとえば、「固定長符号」を用いると、$n$ 文字を表現するのに $\lceil \lg n \rceil$ ビット必要である。こうすると例えば、6個の文字を表現するのに1文字に対して3ビット必要で、a=000, b=001, c=010, d=011, e=100, f=101 というような対応関係を作れる。
固定長符号の良いところは、符号の長さが固定なので、送られてきた文字列の「切れ目」が分かりやすいという点だ。機械的に3文字ずつ切ってやればいい。
ただ、悪いところもある。
それは、データ量が無駄に多いということだ。圧縮効率が悪いとも言いかえれる。
たとえば、6個の文字(a,b,c,d,e,f)を使った100,000文字からなるデータファイルがあり、これを固定長符号に置き換えて送ると、300,000ビット必要になる。
なぜ固定長符号はデータ量が無駄に多いといえるのか?
↓ ↓ ↓ ↓
➡ それは、文字の出現頻度を考慮した設計になっていないからだ。
ふつう、文字列中で登場する文字の出現頻度は、文字ごとに大きく異なる。たとえば、英語における文字の出現頻度は以下のようになっており、e と z ではかなり頻度が異なることが見てわかる。
.svg.png)
後だしでずるいが、文字列というのは普通こういう特徴を持っているため、いま仮に考えている6個の文字を使った100,000文字の文字列データ圧縮にも、仮に出現頻度を設定して考えてみよう。
| a | b | c | d | e | f | |
|---|---|---|---|---|---|---|
| 頻度(千回) | 45 | 13 | 12 | 16 | 9 | 5 |
こんな感じの出現頻度だったとき、出現頻度の高い a に3ビットも割り当てるべきだろうか?
➡ No.
データ圧縮効率のためには、出現頻度の高い文字に短い符号を与え、低い文字には長い符号を与えればよい。こうやって文字ごとに符号語の長さを変えてもよいことにするものを「可変長符号」と呼ぶ。
可変長符号は固定長符号に比べて優れたアイデアだ。
あとで詳しく扱う「ハフマン符号」は可変長符号の一つで、各文字の出現頻度に対して最適なビット文字列の表現方法を見出すことができる。この符号化は貪欲アルゴリズムの一つでもある。
ハフマン符号のアルゴリズムの説明に入る前に、いま考えている6文字の可変長符号の最適な答えだけ与えると、以下のような表になる。
| a | b | c | d | e | f | |
|---|---|---|---|---|---|---|
| 頻度(千回) | 45 | 13 | 12 | 16 | 9 | 5 |
| 可変長符号 | 0 | 101 | 100 | 111 | 1101 | 1100 |
この符号で100,000文字のデータファイルを表現すると、
が必要になる。これは固定長の300,000ビットに比べてデータ量を約25%節約している。
接頭語なし符号
可変長符号にしたことで生まれる疑問がある。
切れ目のないビット文字列に対して、一意に切れ目が定まるのか?
➡ 「接頭語なし符号」であれば、一意に定まる。
接頭語なし符号とは、どの符号語も、別の符号語の接頭語にはならない符号のことである。
ある列 $X=\langle x_1,x_2,\ldots,x_m \rangle$ が与えられているとき、各 $i=0,1,\ldots,m$ について、$X$ の $i$ 番目の接頭語を $X_i=\langle x_1,x_2,\ldots,x_i \rangle$ と定義する。
たとえば、$X=\langle A,B,C,B,D,A,B\rangle$ とすると、$X_4=\langle A,B,C,B\rangle$ である。
これだけだとピンとこないと思うので、具体的に符号になったビット文字列を見て、適切に切れ目を入れて復号できるか試そう。face という文字列で考えると、
| a | b | c | d | e | f | |
|---|---|---|---|---|---|---|
| 可変長符号 | 0 | 101 | 100 | 111 | 1101 | 1100 |
110001001101
これを頭から見ていくと、
1100 / 0 / 100 / 1101 f / a / c / e
と復号できた!もう一つくらい見てみよう。
100011001101 を復号してください。
↓ ↓ ↓ ↓
➡ 100 / 0 / 1100 / 1101 なので、cafe となる。
どの符号語も、ほかの符号語の接頭語にならないので、符号化されたファイルの先頭の符号語にはあいまいさがない。そこで、先頭の符号語を識別し、それを対応するもとの文字に戻し、符号化されたファイルの残りの部分に対してこの処理を繰り返すだけで復号できる。
さて、今回は接頭語なし符号が答えとして与えられていたわけだが、これを作ろうと思ったらどうすればいいのだろうか?
うまい表現がないと、考えるとっかかりがない。
➡ 二分木を使う。
与えられた各文字を葉に対応させる二分木を考えればよい。ある文字に対する2進符号語を、根からこの文字への単純路と解釈する。ただし、
- 0 は 「左の子へ向かう」
- 1 は 「右の子へ向かう」
を意味する。
| a | b | c | d | e | f | |
|---|---|---|---|---|---|---|
| 頻度(千回) | 45 | 13 | 12 | 16 | 9 | 5 |
| 固定長符号 | 000 | 001 | 010 | 011 | 100 | 101 |
| 可変長符号 | 0 | 101 | 100 | 111 | 1101 | 1100 |
この表を表現した二分木は以下の通り。
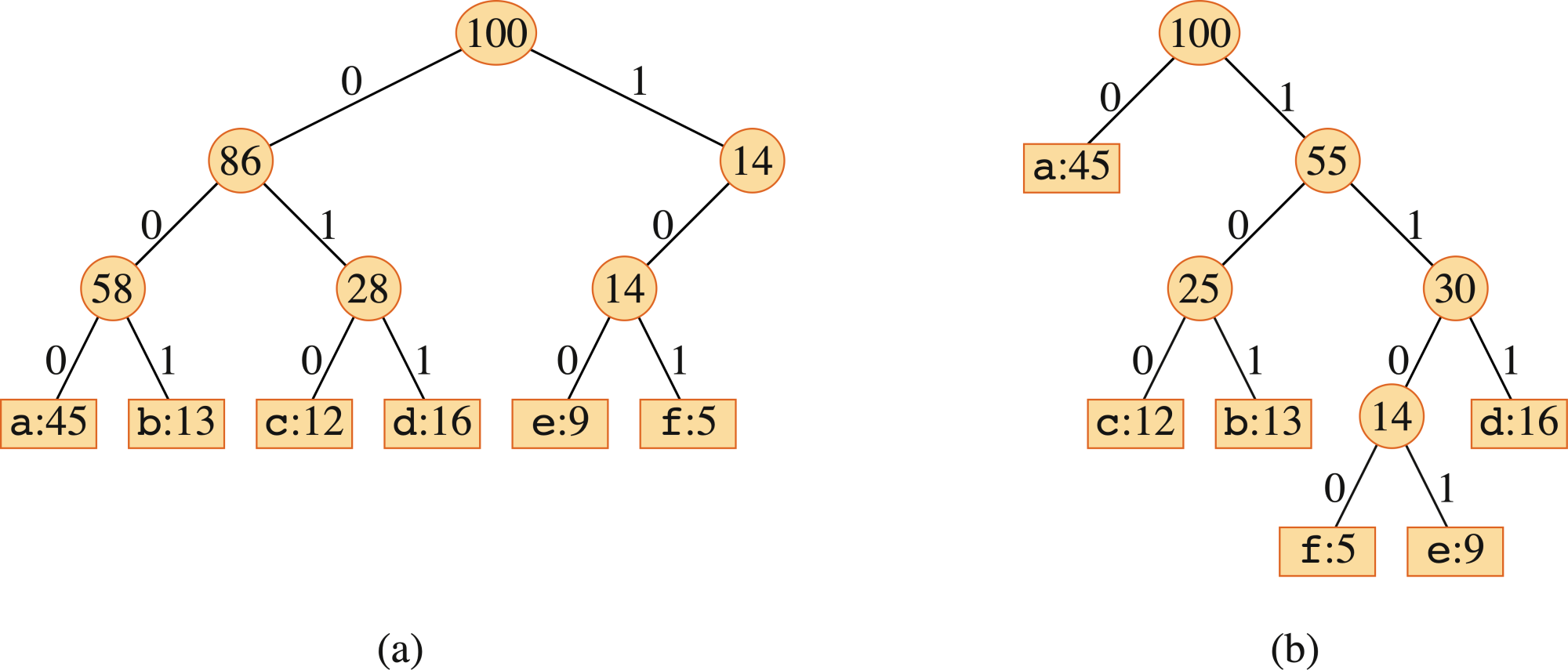
各葉には、文字とその出現頻度がラベルづけられている。すべての出現頻度は単位が1,000である。
葉がソート順に並んでいるわけでもなく、内部節点がキーを含んでいるわけでもないので、これらの木が二分探索木ではないことに注意しよう。
任意のファイルに対する最適な符号は、葉以外のどの節点も必ず2個の子を持つ「全二分木」で表現できる。
先ほど示した固定長符号の木は、10で始まる符号語はあるが、11で始まる符号語はないため全二分木ではない。➡ この木は最適ではない。
全二分木だけを考察の対象にできるので、$C$ を文字集合を表すアルファベットとし、どの文字の出現頻度も正と仮定すると、最適な接頭語なし符号に対する木は、このアルファベットの各文字に対して1個ずつ計 $|C|$ 個の葉と、$|C|-1$ 個の内部節点を持つ。
接頭語なし符号に対応する木 $T$ が与えられると、ファイルを符号化するのに必要なビット数が簡単に計算できる。アルファベット $C$ の各文字 $c$ に対して、そのファイルにおける $c$ の出現頻度を $c.freq$ とする。また、この木における $c$ の葉の深さを $d_{T}(c)$ と表す。$d_{T}(c)$ は文字 $c$ に対する符号語長でもある。
ファイルを符号化するのに必要なビット数は、
これを木 $T$ のコストと定義する。
ハフマン符号の構成

ハフマン符号は、最適な接頭語なし符号を構成する貪欲アルゴリズムである。その正当性の主張は、貪欲選択性と最適部分構造に基づいてできる。
ここでは先にアルゴリズムを提示してから、あとでその正当性を議論する。この方が貪欲選択の理解が容易になるからだ。
手続き HUFFMAN では、$C$ は $n$ 個の文字の集合で、各文字 $c\in C$ は出現頻度を与える属性 $c.freq$ を持つオブジェクトであると仮定する。アルゴリズムは最適な符号に対応する木 $T$ をボトムアップ的に構成する。
すなわち、$|C|$ 個の葉の集合から始め、「統合」操作を $|C|-1$ 回繰り返して最終的な気を構成する。属性 $freq$ をキーとして持つ「min優先度つきキュー $Q$」を統合すべき最も出現頻度の低いほうから2つの要素を識別するために利用する。
これら2つの要素を統合し、統合された2個の要素の出現頻度の和を出現頻度とする新たな要素に置き換える。
HUFFMAN(C)
1. n = |C|
2. Q = C
3. for i = 1 to n-1
4. 新しい節点 z を割り当てる
5. x = EXTRACT-MIN(Q)
6. y = EXTRACT-MIN(Q)
7. z.left = x
8. z.right = y
9. z.freq = x.freq + y.freq
10. INSERT(Q, z)
11. return EXTRACT-MIN(Q) // 木の根のみが唯一の節点として残る
このアルゴリズムの実行結果を具体的な問題インスタンスで図として示す。
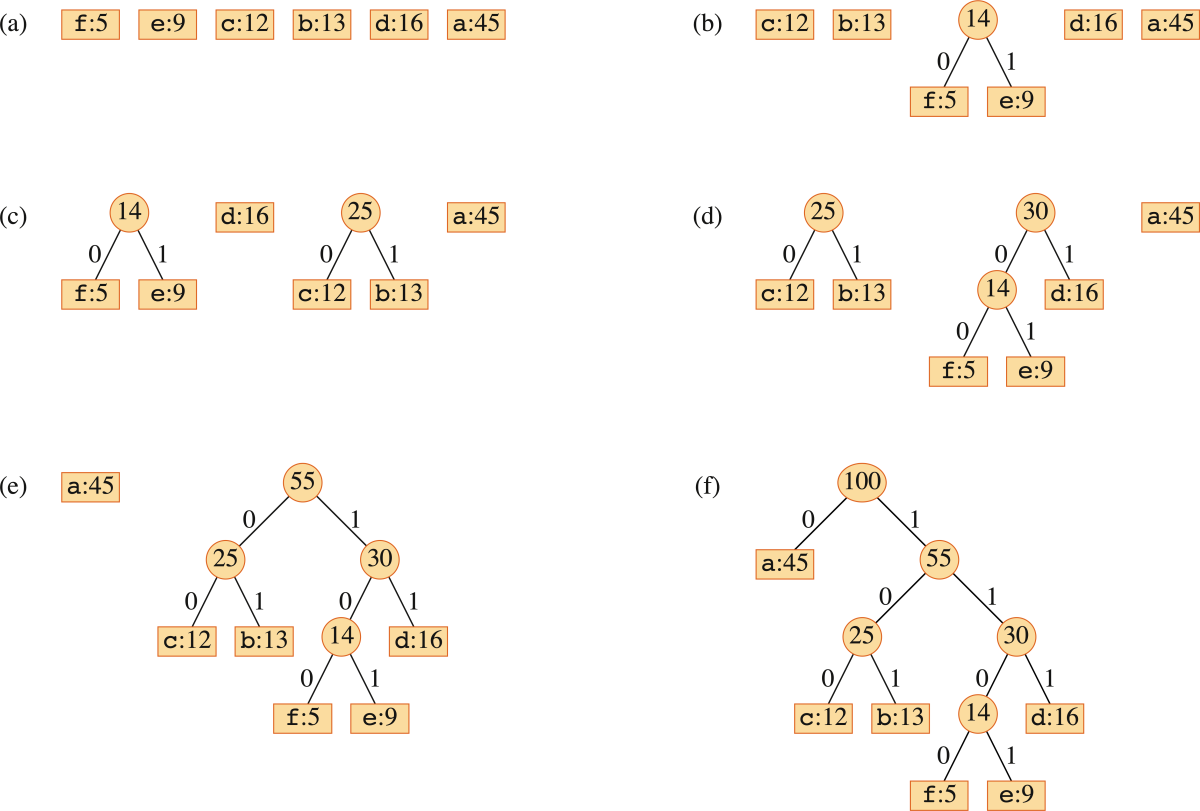
手続き HUFFMAN の実行時間
HUFFMAN のアルゴリズムの実行時間は、min優先度つきキュー $Q$ の実現方法に依存する。ここでは、二分minヒープ(参照:第6章ヒープソート)として実現されていると仮定する。
$n$ 個の文字の集合 $C$ に対して、第2行では第6.3節「ヒープの構築」で検討した手続き BUILD-MIN-HEAP を用いて $O(n)$ 時間で $Q$ を初期化する。
第3~10行の for ループはちょうど $n-1$ 回実行される。ヒープの各操作には $O(\lg n)$ 時間かかるので、このループの実行時間に対する影響は $O(n\lg n)$ 時間である。したがって、$n$ 文字の集合に対する HUFFMAN 全体の実行時間は $O(n\lg n)$ である。
Huffman のアルゴリズムの正当性
アルゴリズムの正当性を証明するために、最適接頭語なし符号を決定する問題が、貪欲選択性と最適部分構造を持つことを証明する。
アルファベットを $C$、各文字 $x\in C$ が出現する頻度を $c.freq$ とする。$C$ の中で出現頻度最小の2つのお文字を $x$ と $y$ とする。このとき、$C$ に対して、$x$ と $y$ に対する符号語が同じ長さで、かつ最後の1ビットを除いて一致する。ある最適接頭語なし符号が存在する。
【証明】
証明の流れとしては、任意の最適接頭語なし符号を表現する木 $T$ をとってきて、$T$ を文字 $x$ と $y$ が深さ最大の兄弟の葉として出現する新しい最適接頭語なし符号木に修正することで証明する。
修正された木に対応する符号では、$x$ と $y$ の符号語は、同じ長さで最後のビットだけが異なる。
$a$ と $b$ を $T$ の中で深さ最大の兄弟の葉に対応する2つの文字とする。一般性を失うことなく以下を仮定できる。
仮定1 $a.freq\le b.freq$ および $x.freq\le y.freq$
$x.freq$ と $y.freq$ は、葉につけられた出現頻度の最小値と2番目に小さい値であり、$a.freq$ と $b.freq$ は仮定を満たす任意の2つの出現頻度なので、$x.freq\le a.freq$ と $y.freq\le b.freq$ が成立する。
証明の以下の部分では、$x.freq=a.freq$ あるいは $y.freq=b.freq$ である可能性がある。しかし、$x.freq=b.freq$ ならば、$a.freq=b.freq=x.freq=y.freq$ であり補題は自明に成立する。
したがって、以下では $x.freq\ne b.freq$ 、すなわち $x=b$ であると仮定する。
仮定2 $x.freq\ne b.freq$ 、すなわち $x=b$
さて、どうやって $T$ から新しい最適接頭語なし符号木に修正するかというと、以下の図のように修正する。

$T$ の $a$ と $x$ の位置を交換して木 $T'$ を作り、次に $T'$ の $b$ と $y$ の位置を交換して木 $T''$ を作る。
$T''$ では $x$ と $y$ は深さ最大の兄弟の葉である。
$a=b$ かつ $y\ne b$ ならば、$T''$ では $x$ と $y$ は深さ最大の兄弟の葉とはならないことに注意せよ。しかし、$x\ne b$ を仮定しているのでこのような事態は起こらない。
ここで、$x$ が出現頻度最小の葉なので、$a.freq-x.freq \ge 0$ であり、$a$ が $T$ の深さ最大の葉なので、$a.freq-x.freq\ge0$ と $d_T(a)-d_T(x)\ge0$ であることに注意すると、式(15.4) より、$T$ と $T'$ のコストの差は、
(式変形を理解するためのメモ書き)

である。同様にして、$y$ と $b$ を交換してもコストは増加しないので、$B(T')-B(T)\ge0$ である。$B(T'')\le B(T')\le B(T)$ かつ $T$ は最適なので、$B(T)\le B(T'')$ である。したがって、$B(T'')=B(T)$ を得る。したがって、$T''$ は $x$ と $y$ が深さ最大の兄弟の葉として表れる最適木であり、補題は証明された。■
補題15.2 により、統合によって最適木を構築する過程は、一般性を失うことなく、出現頻度最小の2文字の等号の貪欲選択から開始できることが主張できる。しかし、どうしてこれが貪欲な選択に当たるのだろうか?
1回の統合のコストを、統合する2つの要素の出現頻度の和とみなすことができる。構成する木の全コストは、実行する等号コストの和である。
各ステップで続き HUFFMAN は、可能なすべての統合の中でコスト最小のものを選択する。
最適接頭語なし符号を構成する問題が、最適部分構造を持つことを次の補題で示す。
アルファベットを $C$、各文字 $c\in C$ の出現頻度を $c.freq$ とする。$C$ の中で出現頻度最小の2つの文字を $x$ と $y$ とする。$C'$ を $C$ から $x$ と $y$ を除去し、代わりに新たに導入された文字 $z$ を加えてできるアルファベット、すなわち $C'=(C-\{x,y\})\cup \{x\}$ とする。
$C'$ に対する出現頻度 $freq$ を、$z.freq=z.freq+y.freq$ と定義することを除いては、$C$ に対する $freq$ と同一であると定義する。$T'$ をアルファベット $C'$ に対する任意の最適接頭語なし符号を表現する木とする。$T'$ の $z$ に対応する葉を $x$ と $y$ を子とする内部節点によって置き換えて得られる木 $T$ とすると、$T$ はアルファベット $C$ に対する最適接頭語なし符号を表現する。
【証明】
まず、式 (15.4) の成分コストを考えることで、木 $T$ のコスト $B(T)$ を木 $T'$ のコスト $B(T')$ によって表現する。
各文字 $c\in C-\{x,y\}$ に対しては、$d_T(c)=d_{T'}(c)$ なので、
である。一方で、$d_{T}(x)=d_T(y)=d_{T'}(z)+1$ なので
である。これらの事実から、
あるいは、
である。
背理法を用いて補題を証明する。$T$ が $C$ に対する最適接頭語なし符号を表現していないと仮定する。このとき、$B(T'') 補題15.2 より一般性を失うことなく、$T''$ は $x$ と $y$ を兄弟として持つと仮定する。$T''$ の $x$ と $y$ の共通の親を出現頻度 $z.freq = x.freq + y.freq$ を持つ葉 $z$ に置き換えることで構成される木を $T'''$ とする。このとき、 であり、これは $T'$ が $C'$ に対する最適接頭語なし符号を表現するという仮定に矛盾する。したがって、$T$ はアルファベット $C$ に対する最適接頭語なし符号を表現する。■ 手続き 【証明】 補題15.2 と 15.3 より明らか。■ コンピュータは記憶を階層化している。本当は、膨大な容量を持っていて、アクセス時間が短いメモリが欲しい。しかし、現実的には という事情がある。あちらを立てればこちらが立たずの状況。 そこで、アクセスの「局所性」を利用する。 よくアクセスされるデータを「主記憶」ではなく「キャッシュ」に入れておくと、データへのアクセス時間を短縮させることができる。 キャッシュは通常32、64、または128倍とからなる「キャッシュブロック」にデータを格納する。仮想記憶システムでは、ディスクに常駐するデータは主記憶がキャッシュであると考えることができる。仮想記憶システムでは、ブロックを「ページ」と呼び、通常サイズは4096バイトである。 コンピュータプログラムの実行に従って、メモリ要求が次々に発生する。ブロック $b_1,b_2,\ldots,b_n$ に含まれるデータへの要求がこの順で発生したと使用。このアクセス列に出現するブロックは必ずしも異なっている必要はなく、実際、どのブロックも普通は複数回にわたってアクセスされる。 たとえば、4つの異なるブロック $p,q,r,s$ にアクセスするプログラムが $s,q,s,q,q,s,p,p,r,s,s,q,p,r,q$ である要求の列を生成することがある。 ある定数 $k$ が存在して、キャッシュには最大 $k$ 個のキャッシュブロックを保持できる。最初の要求の前はキャッシュは空であるとする。各要求によって高々1つのブロックがキャッシュに入り、高々1つのブロックがキャッシュから追い出される。ブロック $b_i$ に対するリクエストがあったとき、次に3つのシナリオのうちのどれかが起こる: 要求されたブロックがキャッシュ内に存在しない後者の2つの状況の時、「キャッシュミスが発生した」という。 $n$ 個の要求列全体に対して、キャッシュミスの数を最小化する。あるいは、同じことだが、キャッシュヒットの数を最大化することである。 キャッシュが $k$ 個未満のブロックしか保持していない状態では、以前に行った決定によらず防ぐことができないキャッシュミスが起きる。これを「初期化ミス」と呼ぶ。 キャッシュミスが起こり、キャッシュが満杯の場合、どのブロックを追い出すかという選択は、理想的には、将来の要求からなる全体の列に対して起こりうるキャッシュミスの数を最小になるようにしなければならない。 典型的には、キャッシング問題は、「オンライン問題」である。すなわち、将来の要求を知らないまま、どのブロックをキャッシュに残すのか?を考えなければならない。 本来的にはオンライン問題として扱うのが正確だが、この章ではあえて「オフライン問題」として読み替えて扱う。つまり、前もってすべての $n$ 個の要求と、キャッシュサイズ $k$ を知っている状況でキャッシュミスの総数を最小化する問題について考えよう。 オフライン版キャッシング問題を解くにはどうすればいいだろう?メタ的なネタバレとして、この章にある以上この問題は貪欲選択性を持っており、貪欲戦略で解くことができるが、貪欲アルゴリズムを思いつくだろうか? ↓
↓
↓
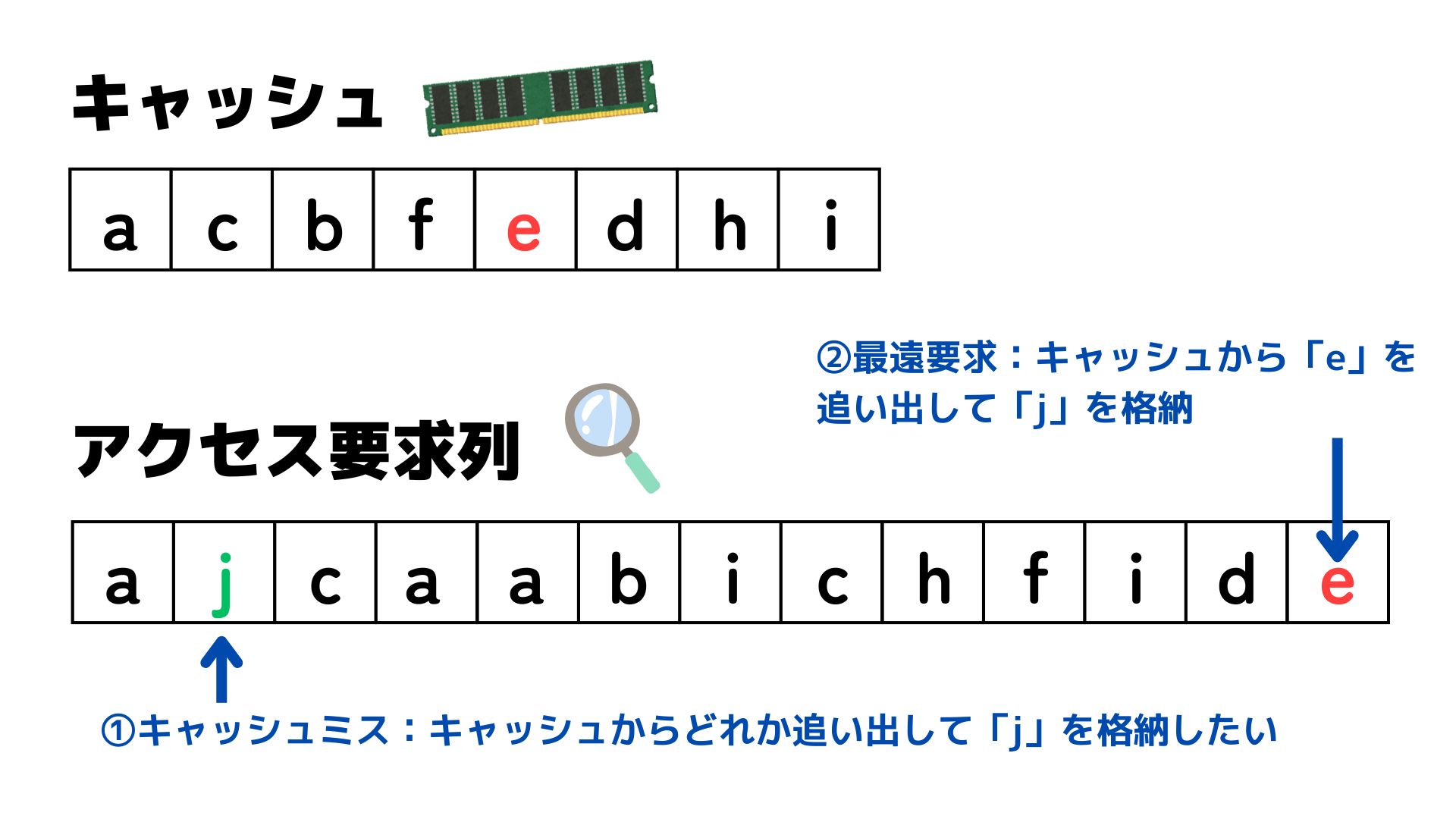
↓ ➡ この問題は「最遠要求優先」と呼ばれる貪欲戦略で解くことができる。 最遠要求優先戦略は、キャッシュに保存されている要素の中で、次のアクセス要求が最も遠いものから順に追い出していくという戦略だ。 この戦略は、「しばらく必要としないものなら、保持しておく必要はないのではなさそう」という直観を反映した戦略だ。 あとで示すが、実際オフラインキャッシング問題は、最適部分構造を持ち、この戦略は貪欲選択性を持つ。 実際の応用を考えると、コンピュータは要求列を前もってはわからないので、オフラインバージョンを考える意味はないのではないか? ➡ そんなことはない。いくつかの意味がある。 ➊ 現実でもある状況においては前もって要求列が分かることがある。たとえば、主記憶(=メインメモリー)をすべてキャッシュとみなし、データ全体が HDD や SSD に置かれているならば、ディスクへの入出力全体の集合を前もって計画するアルゴリズムが存在している。 ❷ 最適アルゴリズムによって生成されるキャッシュミスの回数はオンラインアルゴリズムがどの程度うまく動作しているのか性能評価するための基準として利用できる。これは、第27.3 節(オンラインキャッシュ)で詳しく扱う。 ❸ オフラインキャッシュは、別の現実世界での問題のモデルとしても使える。たとえば、特定のいくつかの場所で行われる $n$ 個のイベントの予定があらかじめ分かっている状況を考える。イベントはある場所で何回も、必ずしも連続ではなく実施されるかもしれない。あなたは $k$ 人のエージェントを差配して、必ず各場所には一人のエージェントを配置するようにし、エージェントが移動する回数を最小化したい。エージェントはキャッシュのブロックに対応し、イベントは要求に対応し、エージェントの移動はキャッシュミスに対応している。 部分問題 $(C,i)$ をキャッシュ状況 $C$ で、ブロック要求 $b_i$ が発生したときに、ブロックに対する要求列 $b_i,b_{i+1},\ldots,b_n$ を処理する問題と定義する。 ここで、$C$ は $|C|\le k$ を満たすブロック集合の部分集合である。部分問題 $(C,i)$ に対する解はブロックの要求 $b_i,b_{i+1},\ldots,b_n$ のそれぞれに対して、どのブロックを追い出すかを決定する列である。部分問題 $(C,i)$ に対する最適解はキャッシュミスの回数を最小化する。 部分問題 $(C,i)$ に対する最適解 $S$ を考え、$C'$ を解 $S$ においてブロック $b_i$ に対する要求を処理した直後のキャッシュの内容とする。 $S'$ をその結果として得られる部分問題 $(C',i+1)$ に対する $S$ の部分解とする。 (1) もし、$b_i$ に対する要求がキャッシュヒットになるなら、キャッシュの内容は変化せず、$C'=C$ である。
(2) もし、$b_i$ に対する要求がキャッシュミスになるなら、キャッシュの内容は変化し、$C'\ne C$ となる。 どっちにせよ、$S'$ は部分問題 $(C',i+1)$ に対する最適解となる。 なぜだろうか? ➡ 背理法で考えよう。 もし、$S'$ が部分問題 $(C',i+1)$ に対する最適解にならなければ、$S'$ よりもキャッシュミスの数が少なくなる部分問題 $(C',i+1)$ に対する別の解 $S''$ が存在するはずである。 このとき、$S''$ と、 $S$ が要求 $b_i$ に対して下した決定を組み合わせることで、$S$ よりもキャッシュミスの数が少なくなる解が得られ、$S$ が部分問題 $(C,i)$ に対する最適解であることに矛盾する。 ということで、$S'$ は部分問題 $(C',i+1)$ に対する最適解となる。(論証おわり) 再帰解を定量化するために、記法をもう少し導入する。 $R_{C,i}$ を、キャッシュ状況が $C$ でブロック $b_i$ に対する要求を処理した直後に出現する可能性のあるすべてのキャッシュ状況の集合とする。 (1) もし、$b_i$ に対する要求がキャッシュヒットになるなら、キャッシュの内容は変わらず $R_{C,i}=\{C\}$ である。 (2) もし、$b_i$ に対する要求がキャッシュミスになるなら、2つの可能性がある。 (2-1) キャッシュが満杯でないとき、すなわち、$|C|< k$ ならば、キャッシュはブロックに蓄えている途中である。したがって、$b_i$ をキャッシュに挿入する。よって、$R_{C,i}=\{C\cup\{b_i\}\}$ である。 (2-2) キャッシュが満杯のとき、すなわち、$|C|=k$ ならば、キャッシュミスが起こる。$R_{C,i}$ は、追い出される候補である $k$ 個のブロックの任意の1つを $b_i$ と入れ替えて得られる $k$ 個のキャッシュ状況の集合である。よって、$R_{C,i}=\{(C-\{x_i\})\cup\{b_i\}: x\in C\}$ である。 たとえば、$C=\\{p,q,r\\},\\; k=3$ でブロック $s$ が要求されるとすると、 部分問題 $(C,i)$ に対する解におけるキャッシュミスの最小数を $miss(C,i)$ と表す。$miss(C,i)$ に対する漸化式は次のようになる。 最遠要求優先戦略が最適解にたどり着くことを示すために、貪欲選択性を示す。 キャッシュ $C$ が $k$ ブロックを含む場合に部分問題 $(C,i)$ を考える。すでに満杯であり、キャッシュミスが起こる。ブロック $b_i$ が要求されたとき、次のアクセスが最遠要求であるような $C$ のブロックを $z=b_m$ とする。 (もし、キャッシュ中のあるブロックが二度と参照されることがなければ、そのような任意のブロックを $z$ とし、ブロック $z=b_m=b_{n+1}$ に対するダミー要求を追加する。) このとき、部分問題 $(C,i)$ に対する最適な解の中に、ブロック $b_i$ に対する要求においてブロック $z$ が追い出されるような解が存在する。 証明、全然理解できてない。😵💫😵💫 【証明】 部分問題 $(C,i)$ に対する最適解を $S$ とする。 $S$ が要求 $b_i$ に対してブロック $z$ を追い出すならば、要求 $b_i$ に対して $z$ を追い出す最適解が存在しているので、定理は証明される。 仮定:
したがって、最適解 $S$ が要求 $b_i$ に対して、$z$ 以外のあるブロック $x$ を追い出したと仮定する。 このとき、部分問題 $(C,i)$ に対する別の解 $S'$ を構築する。 $S'$ は要求 $b_i$ に対して、$x$ の代わりに $z$ を追い出すが、それによりキャッシュミスの回数が $S$ より増えることはない。すなわち、$S'$ もまた最適解である。 異なる解は異なるキャッシュ状況を生み出すので、解 $S$ の下で、あるブロック $b_j$ に対する要求の直前のキャッシュ状況を $C_{S,j}$ とする。また同様に、解 $S'$ では、$C_{S',j}$ とする。 これから、以下の性質を持つ $S'$ の構成法を示す。 性質1:
各 $j=i+1,\ldots,m$ に対して、$D_j=C_{S,j}\cap C_{S',j}$ とする。このとき、$|D_j|\ge k-1$ であり、したがって、キャッシュ状況 $C_{S,j}$ と $C_{S',j}$ は高々1ブロックしか異ならない。もし、それらが異なるならば、$C_{S,j}=D_j\cup \{z\}$ であり、あるブロック $y\ne z$ に対して、$C_{S',J}=D_j\cup \{y\}$ である。 性質2:
各ブロック $b_i,\ldots,b_{m-1}$ の要求に対して、もし解 $S$ にキャッシュヒットがあるなら、解 $S'$ にもキャッシュヒットがある。 性質3:
すべての $j>m$ に対して、キャッシュ状況 $C_{S,j}$ と $C_{S',j}$ は同一である。 性質4:
ブロック $b_i,\ldots,b_m$ の要求列を通して、$S'$ によって生成されるキャッシュミス数は $S$ によって生成されるキャッシュミス数以下である。 これらの性質が各要求に対して成立することを帰納的に証明する。 性質1の証明: 各 $j=i+1,\ldots,m$ に対して $j$ の帰納法で進める。基底段階 $(j=i+1)$ を考える。初期のキャッシュ状況 $C_{S,j}$ と $C_{S',j}$ は同一である。ブロック $b_j$ の要求に対して、解 $S$ は $x$ を追い出し、解 $S'$ は $z$ を追い出す。よって、キャッシュ状況 $C_{S,i+1}$ と $C_{S',i+1}$ は、ちょうど1つのブロックだけが異なり、 であり、$x\ne z$ である。 帰納段階では、$i+1\le j\le m-1$ における、要求 $b_j$ に対する $S'$ のふるまいを定義する。帰納法の仮定より、$b_j$ が要求されたとき、性質1 が成立する。 $z=b_m$ は $C_{S,j}$ に属するブロックの中で最も遠い将来に要求されるブロックなので、$b_j\ne z$ である。いくつかの場合分けを行って考える。 性質2の証明: 性質1の維持に関する上記の議論において、解 $S$ がキャッシュヒットを起こすのは最初の2つの場合に限られる。そしてこの2つの場合では、$S$ がキャッシュヒットを起こしたとき、かつその時に限り、解 $S'$ もキャッシュヒットを起こす。 性質3の証明: $C_{S,m}=C_{S',m}$ ならば、解 $S'$ はブロック $z=b_m$ に対する要求において $S$ と同じ決定を下す。よって、$C_{S,m+1}=C_{S'7',m+1}$ である。 $C_{S,m}\ne C_{S',m}$ ならば、性質1によって、$C_{S,m}=D_m\cup\{z\}$ であり、$C_{S',m}=D_m\cup\{y\}$ である。ここで、$y\ne z$ である。この場合、解 $S$ はキャッシュヒットを起こし、$C_{S,m+1}=C_{S,m}=D_m\cup\{z\}$ となる。解 $S'$ はブロック $y$ を追い出し、ブロック $z$ を取り込むので、$C_{S',m+1}=D_m\cup\{z\}=C_{S,m+1}$ となる。したがって、$C_{S,m}=C_{S',m}$ かどうかにかかわらず、$C_{S,m+1}=C_{S',m+1}$ となり、ブロック要求 $b_{m+1}$ から開始すると、解 $S'$ は $S$ と同じ決定をくだす。 性質4の証明: 性質2によって、ブロック $b_i,\ldots,b_{m-1}$ の要求が発生したとき、解 $S$ がキャッシュヒットを起こしたときはいつも $S'$ もキャッシュヒットを起こす。考察すべき唯一の場合としてブロック要求 $b_m=z$ の場合が残された。ブロック要求 $b_m$ に対して、$S$ がキャッシュミスを起こすならば、$S'$ がキャッシュミスを起こすか否かに関係なく、$S'$ のキャッシュミス数は $S$ のキャッシュミス数以下である。 (4つの性質が各要求に対して成立することの証明おわり) 仮定:
そこで、ブロック $b_m$ に対する要求で $S$ がキャッシュヒットを起こし、$S'$ がキャッシュミスを起こすと仮定する。 ブロック $b_{i+1},\ldots,b_{m-1}$ の少なくとも1つのブロックに対して、ある要求が存在して、その要求の結果 $S$ はキャッシュミスを起こし、$S'$ はキャッシュヒットを起こすことが証明でき、これによってブロック $b_m$ に対する要求で起こったことを相殺できる。 証明は背理法による。 仮定:
ブロック $b_{i+1},\ldots,b_{m-1}$ に対するどのブロック要求においても、$S$ でキャッシュミスが起こり、かつ $S'$ ではキャッシュヒットが起こることはないと仮定する。 まず、ある $j>i$ に対して、キャッシュ状況 $C_{S,j}$ と $C_{S',j}$ が等しくなければ、それ以降も等しいことに注意する。 また、仮定より $b_m\in C_{S,m}$ かつ $b_m\notin C_{S',m}$ であり、$C_{S,m}\ne C_{S',m}$ であることにも注意する。 したがって、ブロック要求 $b_i,\ldots,b_{m-1}$ のどれかに対して $S$ が $z$ を追い出したならば、それ以降は、2つのキャッシュ状況が等しくなり、$C_{S,m}\ne C_{S',m}$ と矛盾するので、どのブロック要求 $b_i,\ldots,b_{m-1}$ に対しても $S$ は $z$ を追い出すことはない。 したがって、各ブロック要求 $b_j$ が発生したとき、あるブロック $y\ne z$ に対して、$C_{S,j}=D_j\cup\{z\}$ かつ $C_{S',j}=D_j\cup\{y\}$ であり、$S$ はあるブロック $w\in D_j$ を追い出す。 さらに、この要求のどれも $S$ でキャッシュミスを起こし(←背理法の仮定より)、$S'$ でキャッシュヒットを起こすことはないので、$b_j=y$ となることはない。 すなわち、ブロック $b_{i+1},\ldots,b_{m-1}$ のそれぞれの要求に対して、要求されたブロック $b_j$ はブロック $y\in C_{S',j}-C_{S,j}$ ではなかったことになる。($b_j\in D_j$ の場合が考慮されていないが、この場合は、$S,S'$ ともにキャッシュヒットであり、キャッシュ状況は変化しない。) これらのブロック要求では、要求 $b_j$ が処理された後、$S'$ の定義より $C_{S',j+1}=D_{j+1}\cup\{y\}$ が成立する。したがって、2つのキャッシュ状況の差は変化しない。 ここで、ブロック要求 $b_i$ の処理直後に戻って考える。$S'$ の定義より $C_{S',i+1}\cup\{x\}\;(x\ne z)$ が成立する。 ブロック要求 $b_m$ に至るまで続くそれぞれのブロック要求に対する $S$ と $S'$ の決定は2つのじゃっしゅ状況の差を変化させない。すなわち、すべての $j=i+1,\ldots,m$ に対して $C_{S',j}=D_j\cup\{x\}$ である。 定義より、ブロック $z=b_m$ に対する要求は $x$ に対する要求の後で発生する。したがって、ブロック $b_{i+1},\ldots,b_{m-1}$ の中の1つはブロック $x$ である。 一方で、$j=i+1,\ldots,m$ に対して、$x\in C_{S',j}$ かつ $x\notin C_{S,j}$ が成立する。したがって、これらの要求に少なくとも1つに対して、$S'$ ではキャッシュヒットが起こり、$S$ ではキャッシュミスが起こることになり、仮定に矛盾する。 まとめると、ブロック $b_m$ に対する要求で解 $S$ にキャッシュヒットが起こり、$S'$ にキャッシュミスが起こるならば、それ以前の要求で逆の結果が起こっていたことになり、解 $S'$ は解 $S$ より多くのキャッシュミスは起こさない。 $S$ は最適と仮定したので、$S'$ も最適である。■ (定理15.5の証明おわり)HUFFMAN は最適接頭語なし符号を生成する。
15.4 オフラインキャッシュ
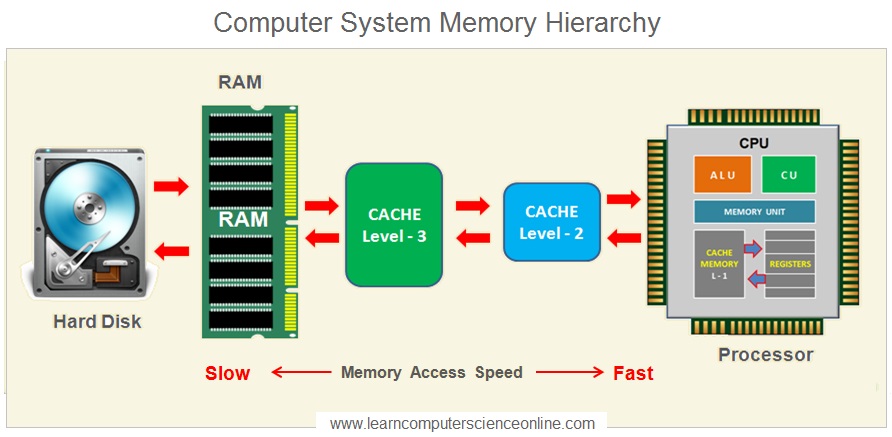
オフラインキャッシングの最適部分構造
貪欲選択性
