14.4 最長共通部分列

なぜ最長共通部分列(LCS)問題を学ぶのか

この節では「最長共通部分列（Longest Common Subsequence: LCS）問題」に取り組む。詳しい定式化は後でやるが、この問題は「似ているけれど同じではない」二つの列（文字列や配列）の共通性を調べるための問題といえる。

LCS問題の解き方を考えることには単なるパズル解き以上の意義がある。具体的には、以下のような意義だ。

  • 🧬 バイオインフォマティクス: DNAやタンパク質の塩基配列を比較し、「配列間の類似度測定」をすることで生物の進化の近縁度合いを調べたり、遺伝的疾患の原因を特定したりする研究の役に立つ。
  • 📄 ファイル比較ツール: diffコマンドのように、2つの文書やプログラムコードが「どこで」「どのように」違うのかを正確に特定する技術の役に立つ。

LCS問題の定式化

意義を把握したところで定式化に移っていこう。

定義：部分列

列 $X = \langle x_1, x_2, \dots, x_m \rangle$ が与えられたとき、別の列 $Z = \langle z_1, z_2, \dots, z_k \rangle$ が $X$ の部分列であるとは、すべての $j = 1, 2, \dots, k$ に対して $x_{i_j} = z_j$ となるような、 $X$ のインデックスの狭義単調増加列 $\langle i_1, i_2, \dots, i_k \rangle$ が存在する場合をいう。

例えば、 $Z = \langle B, C, D, B \rangle$ は、対応するインデックス列が $\langle 2, 3, 5, 7 \rangle$ であるような $X = \langle A, B, C, B, D, A, B \rangle$ の部分列である。

注意

順序は大切だが、必ずしも連続して並んでいる必要はないことに注意が必要だ

定義：共通部分列

2つの列 $X$ と $Y$ が与えられたとき、列 $Z$ が $X$ と $Y$ の両方の部分列であるならば、 $Z$ は $X$ と $Y$ の共通部分列であるという。

例えば、 $X = \langle A, B, C, B, D, A, B \rangle$ かつ $Y = \langle B, D, C, A, B, A \rangle$ の場合、列 $\langle B, C, A \rangle$ は $X$ と $Y$ の両方の共通部分列である。

定義：最長共通部分列（LCS）

共通部分列のうち、最長のものを最長共通部分列（LCS）という。

例えば、列 $\langle B, C, A \rangle$ は $X$ と $Y$ の両方の共通部分列であるが、LCSではない。

一方で、$\langle B, C, B, A \rangle$ と $\langle B, D, A, B \rangle$ は $X$ と $Y$ のLCSである。

LCS問題

  • 入力： $X = \langle x_1, x_2, \dots, x_m \rangle$ と $Y = \langle y_1, y_2, \dots, y_n \rangle$
  • 目標：$X$ と $Y$ の最長共通部分列を見つけること

例えば、次の2つの塩基配列のLCS問題を解いてみよう。

  • $S_1 = \text{ACCGGTCGAGTGCGCGGAAGCCGGCCGAA}$
  • $S_2 = \text{GTCGTTCGGAATGCCGTTGCTCTGTAA}$

これのLCSは $\text{GTCGTCGGAAGCCGGCCGAA}$ である。

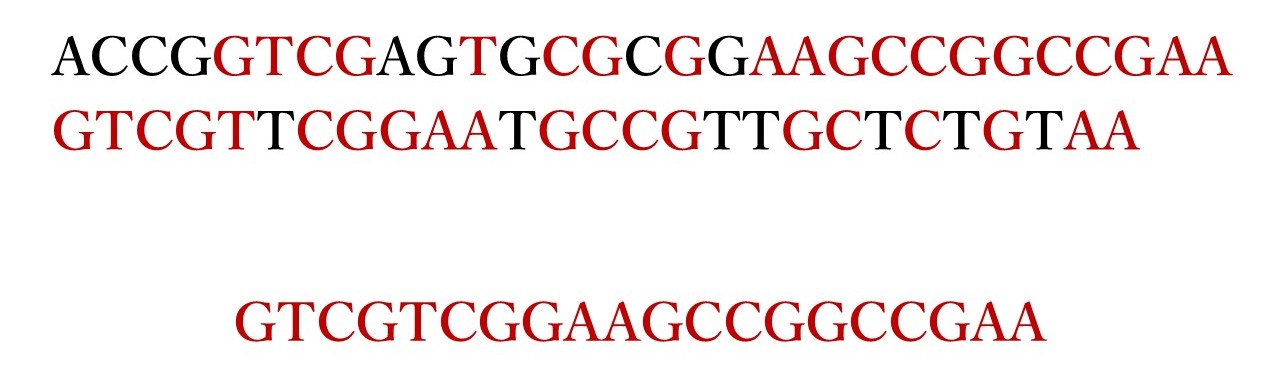
LCS問題を解いていく

問題はまずは簡単に考えてみることが大事なので、いつも通り「しらみつぶし」作戦が通じるかを調べる。

Question

LCS問題をしらみつぶしで解くならどういう手順で解くか？

↓ ↓ ↓

  1. $X$ のすべての部分列を順番に生成する
  2. 生成された部分列が $Y$ の部分列であるかどうかを調べる
  3. これまでに見つけた最長の共通部分列を記憶しておく

こんな感じでいけそうだ。

Question

さて、$X$ には何個の部分列がある？

↓ ↓ ↓

$2^m$ 個

となると、上記のしらみつぶし的なやり方では、$2^m$ 個の部分列を生成してそれに対して作業を行わなきゃいけないから、$X$ が長い列だと現実的にだいぶ厳しい

しかし、LCS問題は定理14.1で示すように最適部分構造の性質を持つ。定理に入る前に1個だけ言葉を定義する。

定義：接頭語

ある列 $X=\langle x_1,x_2,\ldots,x_i\rangle$ が与えられているとき、各 $i=0,1,\ldots,m$ について、$X$ の $i$ 番目の接頭語を $X_i=\langle x_1,x_2,\ldots,x_i\rangle$ と定義する。たとえば、$X=\langle A,B,C,B,D,A,B\rangle$ とすると、$X_4=\langle A,B,C,B\rangle$ である。

定理14.1：LCSの最適部分構造

$X=\langle x_1,x_2,\ldots,x_m\rangle$ と $Y=\langle y_1,y_2,\ldots,y_n\rangle$ を列、$Z=\langle z_1,z_2,\ldots,z_k\rangle$ を $X$ と $Y$ の任意の LCS とする。

  1. $x_m=y_n$ のとき、$z_k=x_m=y_n$ であり、$Z_{k-1}$ は $X_{m-1}$ と $Y_{n-1}$ のLCSである
  2. $x_m\neq y_n$ のとき、$z_k\neq x_m$ ならば $Z$ は、$X_{m-1}$ と $Y$ のLCSである
  3. $x_m\neq y_n$ のとき、$z_k\neq y_n$ ならば $Z$ は、$X$ と $Y_{n-1}$ のLCSである

証明に移る前に、具体的な列でイメージをつかむ。

証明 (1) もし $z_k \neq x_m$ ならば、 $Z$ に $x_m = y_n$ を追加して長さ $k+1$ の $X$ と $Y$ の共通部分列を得ることができる。これは $Z$ が $X$ と $Y$ の最長共通部分列であるという仮定に矛盾する。

したがって、 $z_k = x_m = y_n$ でなければならない。

さて、接頭辞 $Z_{k-1}$ は、 $X_{m-1}$ と $Y_{n-1}$ の長さ $k-1$ の共通部分列である。これがLCSであることを示したい。背理法のために、 $X_{m-1}$ と $Y_{n-1}$ の共通部分列 $W$ で長さが $k-1$ より大きいものが存在すると仮定する。

すると、 $W$ に $x_m = y_n$ を追加することで、長さが $k$ より大きい $X$ と $Y$ の共通部分列が生成され、これは矛盾である。

(2) もし $z_k \neq x_m$ ならば、 $Z$ は $X_{m-1}$ と $Y$ の共通部分列である。

もし $X_{m-1}$ と $Y$ に長さが $k$ より大きい共通部分列 $W$ が存在すれば、 $W$ は $X_m$ と $Y$ の共通部分列でもあり、 $Z$ が $X_m$ と $Y$ のLCSであるという仮定に矛盾する。

(3) 証明は (2) と対称的である。■

定理14.1 から最長共通部分列の特徴づけから、2つの列のLCSが、その2つの列の接頭辞のLCSを内部に含んでいることを示している。したがって、LCS問題は最適部分構造の特性を持つ。後で見るように、部分問題の重複という特性も持つ。

漸化式を立てる

定理14.1は、$X = \langle x_1, x_2, ..., x_m \rangle$と$Y = \langle y_1, y_2, ..., y_n \rangle$のLCSを見つけるには、1つまたは2つの部分問題を調べるべきであることを示唆している。

  • もし $x_m = y_n$ ならば、$X_{m-1}$と$Y_{n-1}$のLCSを見つける必要がある。このLCSに $x_m = y_n$ を連接すると、$X$と$Y$のLCSが得られる。
  • もし $x_m \neq y_n$ ならば、2つの部分問題を解く必要がある。
    • $X_{m-1}$と$Y$のLCSを見つけること
    • $X$と$Y_{n-1}$のLCSを見つけること
    • これら2つのLCSのうち長い方が、$X$と$Y$のLCSとなる。

これらのケースはすべての可能性を網羅しているため、1つの部分問題の最適解が $X$ と $Y$ のLCSの中に必ず出現することが分かった。

次に、LCS問題が部分問題の重複という性質を持つことを確認する。$X$ と $Y$ のLCSを発見するには、 $X$ と $Y_{n-1}$ そして $X_{m-1}$ と $Y$のLCSを見つける必要があるかもしれない。そしてこれらの2つの部分問題は $X_{m-1}$ と $Y_{n-1}$ のLCSを見つけるという部分問題を共有する。同様にして、他の多くの部分問題も、部分問題の共有を伴う。

再帰的な解を導くために、漸化式を立てる。

$X_i$ と $Y_j$ のLCSの長さを $c[i, j]$ と定義しよう。もし $i=0$ または $j=0$ ならば、一方の列の長さが0なので、LCSの長さも0である。LCS問題の最適部分構造から、以下の漸化式が得られる。

LCS問題を解くための漸化式

$$c[i, j] = \begin{cases} 0 & \text{if } i=0 \text{ or } j=0 \\ c[i-1, j-1] + 1 & \text{if } i,j>0 \text{ and } x_i=y_j \\ \max\{c[i, j-1], c[i-1, j]\} & \text{if } i,j>0 \text{ and } x_i \neq y_j \end{cases} \quad (14.9)$$

この漸化式では、問題に関するある条件によって検討すべき部分問題が変化することに注意してほしい。

$x_i=y_j$ である場合、部分問題である $X_{i-1}$ と $Y_{j-1}$ のLCSを見つける部分問題が現れ、この部分問題を必ず検討する。

$x_i\neq y_j$ である場合、$X_i$ と $Y_{j-1}$ のLCSを見つける部分問題と、$X_{i-1}$ と $Y_j$ のLCSを見つけるという2つの部分問題を検討することになる。

前半でやった動的計画法のアルゴリズムでは、問題内の条件によって部分問題を検討から除外することはなかった。

LCS発見問題以外にも、問題内の条件に基づいて部分問題を除外できる動的計画アルゴリズムが存在する。例えば、編集距離問題（章末問題14-5）もこの性質を持つ。

漸化式を解く

式 (14.9) を素直に再帰的に求めるアルゴリズムを考えると以下のようになる。

LCS-NAIVE(X, Y, m, n)
1	return LCS-RECURSIVE(m, n)

LCS-RECURSIVE(i, j)
2	if i == 0 or j == 0:
3		return 0
	
4	if X[i] == Y[j]:
5		return 1 + LCS-RECURSIVE(i - 1, j - 1)
6	else:
7		return max(
8			LCS-RECURSIVE(i    , j - 1),
9			LCS-RECURSIVE(i - 1, j    )
10			)

これは同じ部分問題を何度も計算するので、時間計算量は $O(2^{(m+n)})$ くらい？で指数時間オーダーになる。素直に再帰だと重複多くてカスい。重複していない部分問題の個数分オーダーにしたい。

Question

重複していない部分問題の個数はだいたい幾つだろう？

↓ ↓ ↓

LCS問題は $0 \le i \le m$ かつ $0 \le j \le n$ について $c[i, j]$ を計算するという、$\Theta(mn)$ 個の異なる部分問題しか持たない。

それなら $0 \le i \le m$ かつ $0 \le j \le n$ について $c[i, j]$ を下から計算していけばいいので…… 

LCS-LENGTH(X, Y, m, n)
1  let b[1 : m, 1 : n] and c[0 : m, 0 : n] be new tables
2  for i = 1 to m
3      c[i, 0] = 0
4  for j = 0 to n
5      c[0, j] = 0
6  for i = 1 to m  // 行優先で表の値を計算する
7      for j = 1 to n
8          if xi == yj
9              c[i, j] = c[i - 1, j - 1] + 1
10             b[i, j] = "↖"
11         elseif c[i - 1, j] >= c[i, j - 1]
12             c[i, j] = c[i - 1, j]
13             b[i, j] = "↑"
14         else c[i, j] = c[i, j - 1]
15             b[i, j] = "←"
16 return c and b

PRINT-LCS(b, X, i, j)
1  if i == 0 or j == 0
2      return  // LCSの長さは0
3  if b[i, j] == "↖"
4      PRINT-LCS(b, X, i - 1, j - 1)
5      print xi  // yjと同じ
6  elseif b[i, j] == "↑"
7      PRINT-LCS(b, X, i - 1, j)
8  else PRINT-LCS(b, X, i, j - 1)

この手続きは、表 $c[0:m,0:n]$ に $c[i,j]$ 値を保存するが、それらの計算は行優先で行う。

行優先とは？

**行優先（Row-major order）**とは、2次元配列の要素にアクセスしたり、処理したりする際の順序の一つです。具体的には、まず最初の行の要素を左から右へ順番に処理し、次に2番目の行、3番目の行と、行を上から下へ移動しながら各行の要素を処理していく方法を指します。

このアルゴリズムの文脈では、c表とb表の値を計算する際に、c[1,1], c[1,2], c[1,3], …と第1行を埋めていき、それが終わるとc[2,1], c[2,2], c[2,3], …と第2行を埋めていく、という順序で計算が進むことを意味します。これは、for i（行のループ）が外側にあり、for j（列のループ）が内側にあることからもわかります。

上図は $X=\langle A,B,C,B,D,A,B \rangle$ と $Y=\langle B,D,C,A,B,A\rangle$ を入力とする手続き LCS-LENGTH が計算した表 $c$ と $b$ を表現した図である。$i$ 行と $j$ 列の箱は $c[i,j]$ 値と $b[i,j]$ 値を表現する矢印を含む。

表の右下隅の $c[7,6]$ の値 $4$ は、$X$ と $Y$ のLCS $\langle B,C,B,A\rangle$ の長さである。$i,j>0$ のとき、$c[i,j]$ の値は $x_i=y_j$ の成否と $c[i,j]$ より前に計算する $c[i-1, j], c[i,j-1], c[i-1,j-1]$ の値だけに依存する。

LCSの構成

$b[i,j]$ が定める矢印を右下隅からたどれば（たどれる経路を青色で示す）LCSの要素が再構成できる。青いセルの中に示された経路上に現れる「↖」を含む（強調表示された）要素は、$x_i=y_j$ がLSの要素であることを示す。

この方法では、LCSの要素が逆順で得られる。再帰的な手続きPRINT-LCSは、$X$と$Y$のLCSを正しい順序で出力する。

最初の呼び出しはPRINT-LCS(b, X, m, n)である。図のb表に対して、この手続きは $BCBA$ を出力する。この手続きは、再帰呼び出しごとに $i$ または $j$（あるいは両方）を少なくとも1つ減らすため、$\Theta(m + n)$時間で実行される。

コードの改良

アルゴリズムを開発した後、その使用する時間や空間を改善できることにしばしば気づくことがある。いくつかの変更は、改善はするものの漸近的な性能向上にはつながらない定数倍の改善をもたらす。しかし、時間と空間において大幅な漸近的な節約をもたらす変更もある。

Question

定数倍の改善としてどんなものが思いつくだろう？

↓ ↓ ↓

LCSの構成に使った b 表を削除してしまおう。

というのも、$c[i,j]$ の各要素は

  • $c[i-1,j-1]$
  • $c[i-1,j]$
  • $c[i,j-1]$

の3要素だけに依存しており、b 表を参照しなくても、これら3つの値の中から $c[i,j]$ の計算に使われた値を $O(1)$ で決定できる。

PRINT-LCS を以下のようなコードで置き換えてやれば復元できる。

TRACEBACK(c, X, Y, m, n):
1	i ← m; j ← n; S ← empty stack
2	while i > 0 and j > 0:
3		if X[i-1] == Y[j-1]:
4			push X[i-1] to S
5			i ← i-1; j ← j-1
6		elseif c[i-1, j] >= c[i, j-1]:
7			i ← i-1
8		else:
9			j ← j-1
10	return reverse(S)  // あるいはスタックをpopしながら出力

ループ中で毎回 i か j（あるいは両方）が 1 ずつ減るので、反復回数は高々 m + n 回で、各反復の処理は定数時間なので、再構成にかかる計算資源の漸近的消費は、

  • 時間計算量：$O(m + n)$
  • 補助空間量：スタック S に LCS 長（$L$）だけ積むので $O(L)$ だが、出力をpopしながら直接吐けば $O(1)$ で済む

b 表を消去しているので、空間資源を $\Theta(mn)$ 節約しているが、c 表は消去できないので、結局アルゴリズム全体での空間計算量は $\Theta(mn)$ で変わらない。しかし、定数倍は改善された。

Question

実は、LCSの構築を諦めれば、LCS-LENGTH の漸近的空間計算量を削減する方法がある。どうすればよいだろう？

↓ ↓ ↓

一度にc表の2行、すなわち計算中の行と前の行だけが必要であるという事実を用いればよい。

つまり、行 i を計算するときに必要なのは「前の行 (i-1)」だけなので、 2 行（あるいは 1 行＋変数）のみを保持すれば、LCS の「長さ」は計算できる。

prev[0:n] = 0
curr[0:n] = 0
for i = 1 to m:
    for j = 1 to n:
        if X[i - 1] == Y[j - 1]:
            curr[j] = prev[j - 1] + 1
        else:
            curr[j] = max(prev[j], curr[j - 1])
    swap(prev, curr)
return prev[n]

これで c 表さえ消去できた。（LCSの構築はできないけど）

空間計算量は $O(n)$ だ。

Question

実は、LCSの構築を諦めれば、LCS-LENGTH の漸近的空間計算量を削減する方法がある。どうすればよいだろう？（練習問題14.4-2）

↓ ↓ ↓

左上の値しか使わないんだからそれだけ一つの変数に保存しておいて、1行＋1セルにしとけばさらに空間効率が良くなる。

dp[0 : n] = 0          // dp[j] は「前の行の値」を保持しつつ更新される

for i = 1 to m:
    diag = 0           // c[i-1, j-1] を保持
    for j = 1 to n:
        tmp = dp[j]    // 次の j で使うため、元の c[i-1, j] を退避
        if X[i - 1] == Y[j - 1]:
            dp[j] = diag + 1
        else:
            dp[j] = max(dp[j], dp[j - 1])  // 上 vs 左
        diag = tmp      // 次ループ用に左上を更新
return dp[n]

14.5 最適二分探索木

翻訳プログラムを作ろう

英語からラトビア語へテキストを翻訳するプログラムを設計しているとする。現代的にやるならDNN的手法を使うことになるが、ここでは英語とラトビア語の単語の対応をとった辞書データを用意して、それをもとに逐語訳的に翻訳する簡単なシステムをつくることにする。

このとき、文章に出現する各英単語について、同じ意味のラトビア語の単語を探索する必要がある。

英単語をキーとし、対応するラトビア語の単語を付随データとして持つ$n$個のオブジェクトからなる二分探索木を構築することでこの探索操作は実現できる。

文章中に現れる英単語のそれぞれに対して探索をするので、総探索時間をできる限り少なく抑えたい。

1回の英単語の出現に対して探索時間を $O(\lg n)$ で抑えることは、2色木やほかの平衡二分探索木を用いることで実現できる。

しかし、単語が出現する回数は単語によって異なる。平衡二分探索木は「キーの大小関係」には公平だが、「よく使う単語を根の近くに置く」とは限らない。

結果として、“the” のような頻出単語が深い位置、“naumachia"のようなレア単語が根付近という非効率な配置になるかもしれない。

ちなみに naumachia の意味は、古代ローマの円形闘技場で開催された興行の一つで、闘技場に水を張り、歴史上の有名な海戦を再現したもの。

本題に戻る。

あるキーを二分探索木の中から発見する際に訪れる節点数は、このキーを含む節点の深さに 1 を加えたものなので、頻出単語が深い位置でレア単語が根に近い位置にあるような探索木では、翻訳速度を低下させてしまう。

頻繁に出る単語が深い位置にあると、毎回その単語を探すたびに多くの節点をたどる＝時間がかかるという話だ。

たとえば、

  • “the”：出現 10,000 回、深さ 8 ⇒ 1回9ノード×10,000 = 90,000ノード
  • “naumachia”：出現 2 回、深さ 1 ⇒ 1回2ノード×2 = 4ノード
    → 合計 90,004 ノード訪問

こういう場合、“the” を浅くすれば、この合計は大きく減る。

問題設定の定式化

Question

では、各単語がどれくらいの頻度で出現するかが分かっているとして、全ての探索において訪れるノード数を最小化するような二分探索木（最適二分探索木）を構成するにはどうすればよいか？

↓ ↓ ↓

探索コストの期待値を最小化するような木を構築すればよい。具体的に考えるために、問題設定を形式的に表そう。

最適二分探索木の構成問題

【各単語がどれくらいの頻度で出現するかが分かっている】

$k_1 \lt k_2 \lt ... \lt k_n$ となるような $n$ 個の異なるキーの列 $K = \{k_1, k_2, ..., k_n\}$ が与えられたとき、これらのキーを含む1つの二分探索木を作る。各キー $kᵢ$ について、任意の探索がキー $k_i$ に対するものである確率 $p_i$ が与えられている。

【探索木に存在しないキーの扱い】

いくつかの探索は $K$ にない値に対するものである可能性があり、そのために $n+1$ 個の「ダミー」キー $d_0, d_1, d_2, ..., d_n$ も用意する。これらは $K$ にない値を表す。

特に、$d_0$ は $k_1$ より小さい全ての値を表し、$d_n$ は $k_n$ より大きい全ての値を表し、$i = 1, 2, ..., n-1$ に対して、ダミーキー $d_i$ は $k_i$ と $k_{i+1}$ の間の値を表す。各ダミーキー $d_i$ について、探索が $d_i$ で終わる確率 $q_i$ も与えられている。

【探索は成功と失敗のどっちか】

$$\sum_{i=1}^{n} p_i + \sum_{i=0}^{n} q_i = 1 \tag{14.10}$$

【探索の期待コスト】

キーとダミーキーの探索確率を知ることで、二分探索木における探索の期待コストを決定できる。$T$ における探索の実際のコストは、探索で見つかったノードの深さに1を加えた、すなわち訪れたノードの数であると仮定する。したがって、$T$ における探索の期待コストは次のようになる。

$$\begin{aligned}\mathbb{E}[T\text{ での探索コスト}] &= \sum_{i=1}^{n} (\text{depth}_T(k_i) + 1) \cdot p_i + \sum_{i=0}^{n} (\text{depth}_T(d_i) + 1) \cdot q_i \\ &= 1 + \sum_{i=1}^{n} \text{depth}_T(k_i) \cdot p_i + \sum_{i=0}^{n} \text{depth}_T(d_i) \cdot q_i \end{aligned}\quad(14.11)$$

ここで、$\text{depth}_T$ は $T$ におけるノードの深さを示す。最後の等式は、式 (14.10) から導かれる。

与えられた確率の集合に対して、期待探索コストが最小となるような二分探索木を構築したい。そのような木を最適二分探索木と呼ぶ。

図14.9(a) は、期待コスト2.80の1つの二分探索木を示している。図14.9(b) の木は同じキー集合に対して期待コスト2.75であり、この図のキャプションで与えられた確率に対して最適である。この例は、最適二分探索木が必ずしも全体の高さが最小の木であるとは限らないことを示している。また、最適二分探索木が、最も確率の高いキーを常に根に持つわけでもない。ここでは、最も確率の高いキーは $k_5$ であるが、最適木の根は $k_2$ である。（$k_5$ が根である最適木の期待コストは2.85である。）

行列連鎖乗算と同様に、全ての可能性を網羅的にチェックしても効率的なアルゴリズムは得られない。というのも、$n$個のノードを持つ二分探索木の数 $bₙ$ は、$n$ 番目のカタラン数によって与えられるからだ。

つまり、$n$個のノードを持つ二分探索木の数は $\Omega(4^n/n^{3/2})$ だということだ 。全探索はムリそうだ。ここでは、この問題を動的計画法でより効率的に解く方法を示す。

最適部分構造

いつも通り、最適部分構造の特徴づけを行う。

最適二分探索木の任意の部分木は、連続した範囲のキー $k_i, \dots, k_j$（ただし $1 \le i \le j \le n$）を含んでいなければならない。さらに、部分木は、その葉としてダミーキー $d_{i-1}, \dots, d_j$ を持っていなければならない。

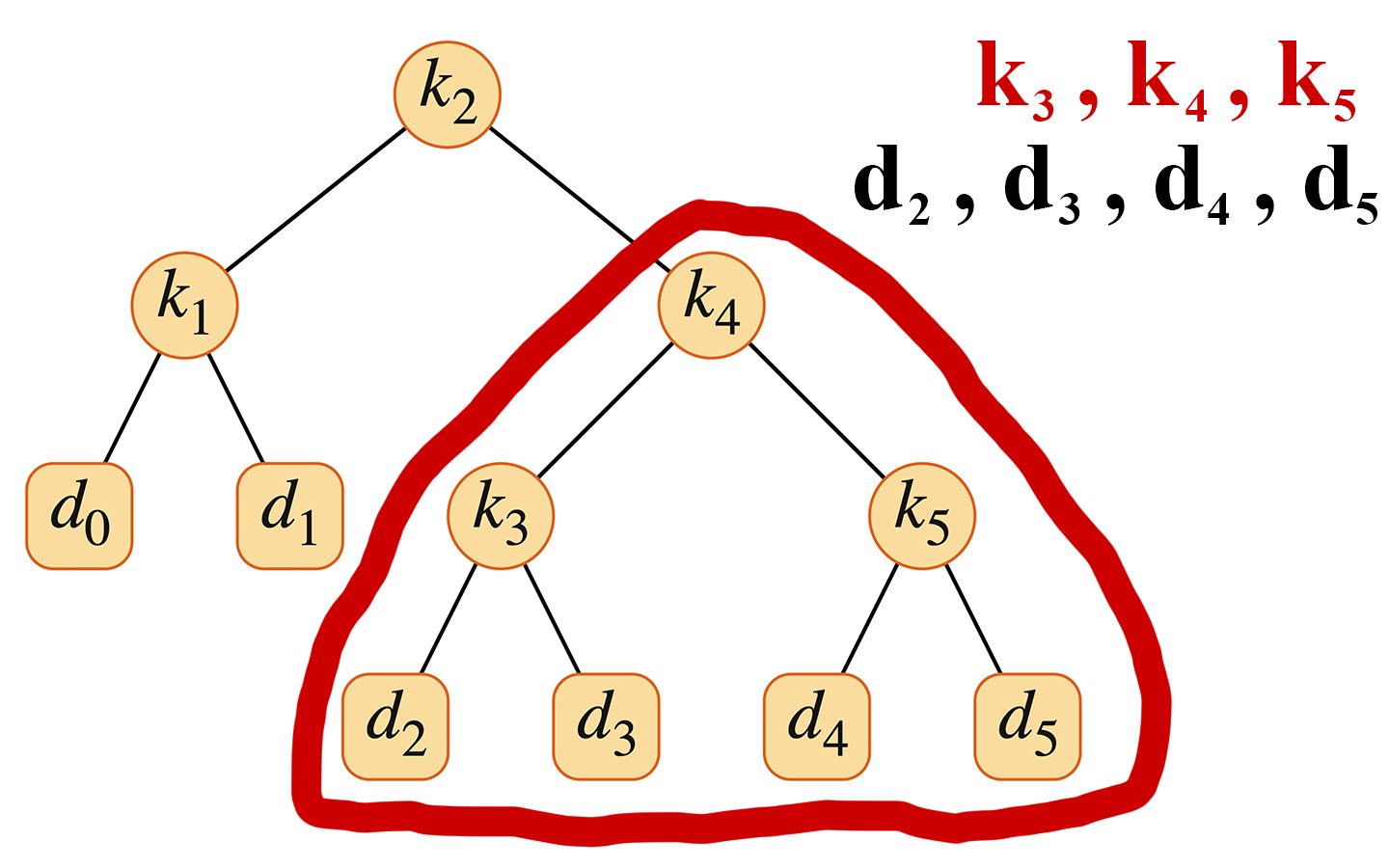
ここに、最適部分構造を見いだせる。

もし最適二分探索木 $T$ がキー $k_i, \dots, k_j$ を含む部分木 $T'$ を持つならば、この部分木 $T'$ はキー $k_i, \dots, k_j$ とダミーキー $d_{i-1}, \dots, d_j$ を持つ部分問題に対して最適でなければならない。切り貼り論法で示せる。

切り貼り論法

ある部分問題の解が最適ではないと仮定し、矛盾を導くことで証明する。つまり、最適ではないと仮定した部分問題の解を「切り取り」、最適解に「張り替える」と元の問題に対してより良い解を得られるので、与えられた元の問題の解は最適であるという仮定に対する矛盾が導かれる証明だ。

簡単な証明 もし $T'$ よりも期待コストが低い部分木があったとすれば、$T'$ を切り取ってその新しい部分木を貼り付けることで、$T$ よりも期待コストが低い二分探索木が得られ、これは $T$ の最適性に矛盾する。■

最適部分構造を手に入れたので、部分問題からの最適解をどのように構築するかを次に示す。

キー $k_i, \dots, k_j$ が与えられたとき、これらのキーのうちの1つ、例えば $k_r$ ($i \le r \le j$) が、これらのキーを含む最適部分木の根である。

以下の例でいうと、$k_r = k_4$ である。

根 $k_r$ の左部分木はキー $k_i, \dots, k_{r-1}$（およびダミーキー $d_{i-1}, \dots, d_{r-1}$）を含み、右部分木はキー $k_{r+1}, \dots, k_j$（およびダミーキー $d_r, \dots, d_j$）を含む。

$i \le r \le j$ の範囲で候補となるすべての根 $k_r$ を調べ、キー $k_i, \dots, k_{r-1}$ を含むすべての最適二分探索木と、キー $k_{r+1}, \dots, k_j$ を含むすべての最適二分探索木を決定する限り、最適な二分探索木を見つけることが保証される。

Warning

理解すべき細かい話が一つある。それは「空の」部分木に関するものである。

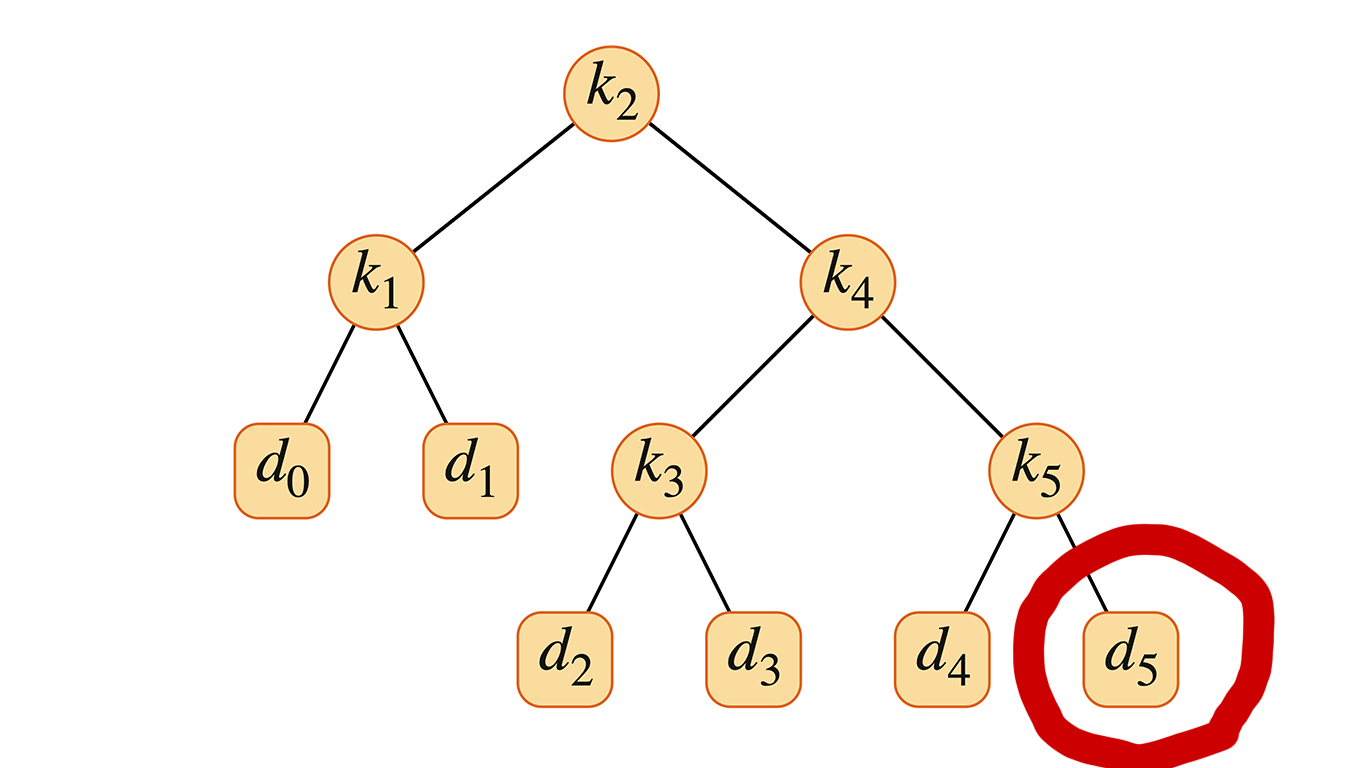
部分木がキー $k_i, \dots, k_j$ を持つとして、$i=j+1$ となるように $k_i$ を根として選択したとしよう。上記の議論によれば、$k_i$ の左部分木はキー $k_i, \dots, k_{i-1}$ を含み、これは全くキーを含まない。

同様に、その部分木はダミーキー $d_i, \dots, d_{i-1}$ を含み、これもダミーキーを含まない。そこで、キー $k_i, \dots, k_{i-1}$ を含む部分木が実際のキーは持たず、単一のダミーキー $d_{i-1}$ のみを含むという解釈を採用する。同様に、$k_j$ を根として選択した場合、$k_j$ の右部分木はキー $k_{j+1}, \dots, k_j$ を含む。この右部分木は実際のキーは持たず、ダミーキー $d_j$ のみを含む。

漸化式を立てる

最適解の値を再帰的に定義するために、キー $k_i, \dots, k_j$ を含む最適二分探索木を見つける部分問題を考える。ここで、$1 \le i \le j \le n$ である。ただし、$j=i-1$ の場合は、実際のキーはなく、ダミーキー $d_{i-1}$ のみを持つ。

目標

$e[i, j]$ を、キー $k_i, \dots, k_j$ を含む最適二分探索木の期待探索コストとする。最終的な目標は、$e[1, n]$、つまり、すべての実際のキーとダミーキーに対する最適二分探索木の期待探索コストを計算することである。

【 $j=i-1$ の場合】

簡単なケースは $j=i-1$ のときである。そのとき、部分問題はダミーキー $d_{i-1}$ のみからなる。期待探索コストは $e[i, i-1] = q_{i-1}$ である。

【 $j\ge i$ の場合】

$j \ge i$ のとき、根 $k_r$ を $k_i, \dots, k_j$ から選択し、キー $k_i, \dots, k_{r-1}$ をその左部分木として、キー $k_{r+1}, \dots, k_j$ をその右部分木として持つ最適二分探索木を作る必要がある。

ある部分木がある節点の部分木となったときの期待探索コストはどうなるか？

部分木内の各ノードの深さは1ずつ増加する。したがって、式(14.11)により、部分木の期待探索コストは、その部分木内のすべての確率の合計だけ増加する。キー $k_i, \dots, k_j$ について、この確率の合計を $w(i, j)$ と書く。

$$ w(i, j) = \sum_{l=i}^{j} p_l + \sum_{l=i-1}^{j} q_l \tag{14.12} $$

したがって、$k_r$ がキー $k_i, \dots, k_j$ を含む最適部分木の根である場合、次式が成り立つ。

$$ e[i, j] = p_r + \underbrace{(e[i, r-1] + w(i, r-1))}_{\text{左部分木}} + \underbrace{(e[r+1, j] + w(r+1, j))}_{\text{右部分木}} $$

$w(i, j) = w(i, r-1) + p_r + w(r+1, j)$ であることを利用すると、$e[i, j]$ を次のように書き換えることができる。

$$ e[i, j] = e[i, r-1] + e[r+1, j] + w(i, j) \tag{14.13} $$

できた漸化式がこちら

漸化式(14.13)は、使用する根ノード $k_r$ を知っていることを前提としている。もちろん、僕たちはどのノードを根として使用すべきか知らない。したがって、最小の期待探索コストを与える根を選択する必要がある。これにより、最終的な漸化式が得られる。

最適二分探索木を見つけるための漸化式

$$e[i,j] = \begin{cases} q_{i-1} & \text{if } j = i-1 \\ \displaystyle\min_{i \le r \le j} \{e[i,r-1] + e[r+1,j] + w(i,j)\} & \text{if } i \le j \end{cases} \tag{14.14}$$

$e[i,j]$ の値が、最適二分探索木における期待探索コストを与える。最適二分探索木の構造を追跡するために、キー $k_r$ がキー $k_i, \dots, k_j$ （$1 \le i \le j \le n$）を持つ最適二分探索木の根となるインデックス $r$ として $\text{root}[i,j]$ を定義する。$\text{root}[i,j]$ の値の計算方法は後で見るが、これらの値から最適二分探索木を構築することは、練習問題14.5-1に残されている。

漸化式を解く

この時点で、最適二分探索木と行列連鎖積問題の特性づけの間にいくつかの類似点に気づいたかもしれない。

行列連鎖積問題との類似点

  • 分割の仕方
    • 最適二分探索木：根の候補 $r\in[i,j]$ を選ぶ
    • 行列連鎖積：かっこわけ位置 $k \in [i, j-1]$ を選ぶ
  • 漸化式の形：左の区間＋右の区間＋結合コスト
    • 最適二分探索木：$e[i,j] = \begin{cases} q_{i-1} & (j = i-1) \\ \displaystyle\min_{i \le r \le j} \{e[i,r-1] + e[r+1,j] + w(i,j)\} & (i \le j) \end{cases}$
    • 行列連鎖積：$m[i,j]= \begin{cases} 0 \quad &(i=j) \\ \displaystyle{\min_{i \le k\lt j} ​\{ m[i,k] + m[k+1,j]+p_{i−1​}p_k​ p_j​ \}} ​\quad &(i\lt j) \\ \end{cases}$

式(14.14)の直接的な再帰的実装は、行列連鎖乗積のアルゴリズムと同様に非効率になる。代わりに、表 $e[1 : n+1, 0 : n]$ に $e[i,j]$ の値を格納する方法で解く。ボトムアップ方式の動的計画法だ。小さい部分木の最適な根を求めて、それを大きい部分木に持っていけば、最適な根の配置で全体の木が構成できる。

ここで、表のインデックスの始まりと終わりが $i,j$ でそれぞれズレていることに注意。

Warning

最初のインデックスの値は $n+1$ まで動く必要がある。

これは、部分木がダミーキー $d_n$ だけを含む場合のために、$e[n+1, n]$ を計算して保存する必要があるからである。

Warning

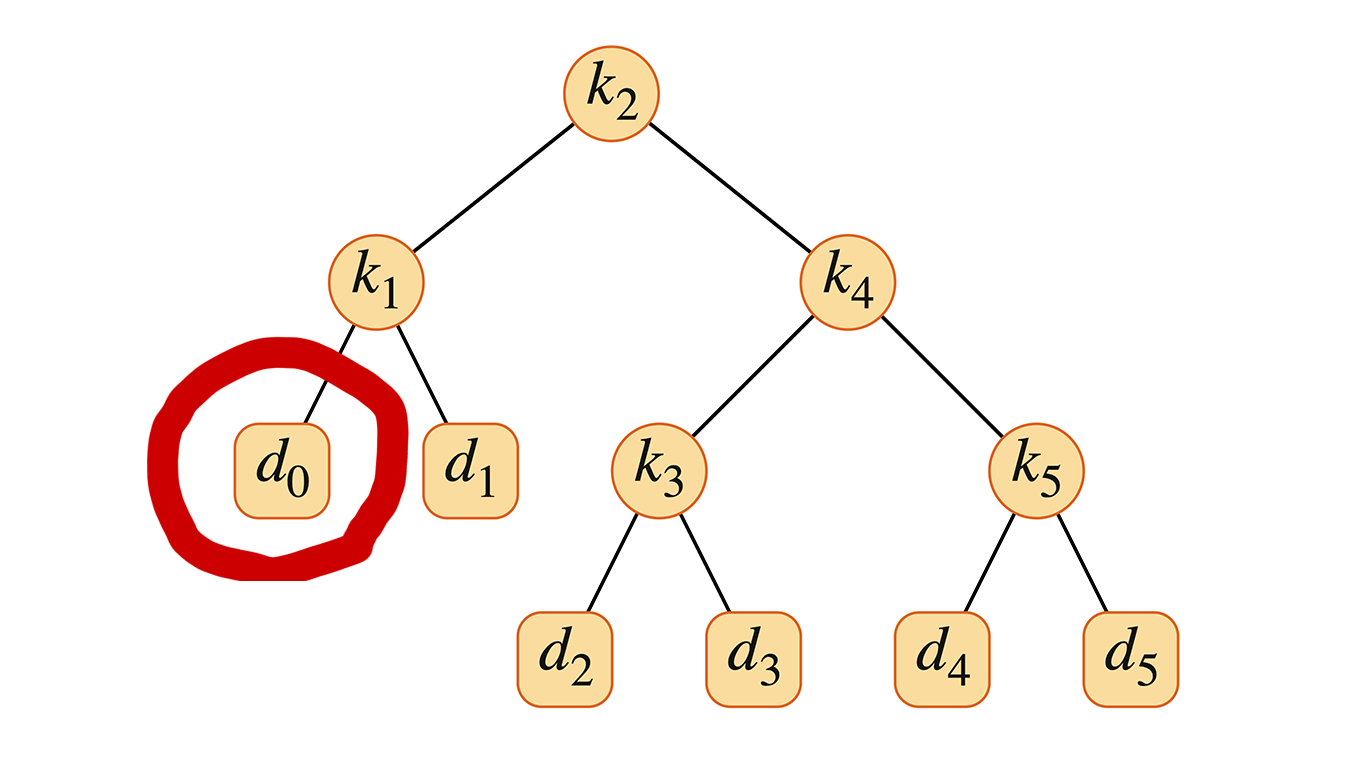
一方で、第2のインデックスは0から始める必要がある。

これは、ダミーキー $d_0$ のみを含む部分木を計算する必要があるためであり、そのためには $e[1, 0]$ を計算する必要があるからである。

これで両端のダミーにも対応するすべての空の区間も含んで表に保存することができます。

僕たちは、$j \ge i - 1$ を満たす要素 $e[i,j]$ のみを使用する。また、表 $\text{root}[i,j]$ は、キー $k_i, \dots, k_j$ を含む部分木の根を記憶するためにも使い、この表は $1 \le i \le j \le n$ を満たす要素だけを利用する。（図の緑色のところだけ使う。対角要素がダミーノードに対応）

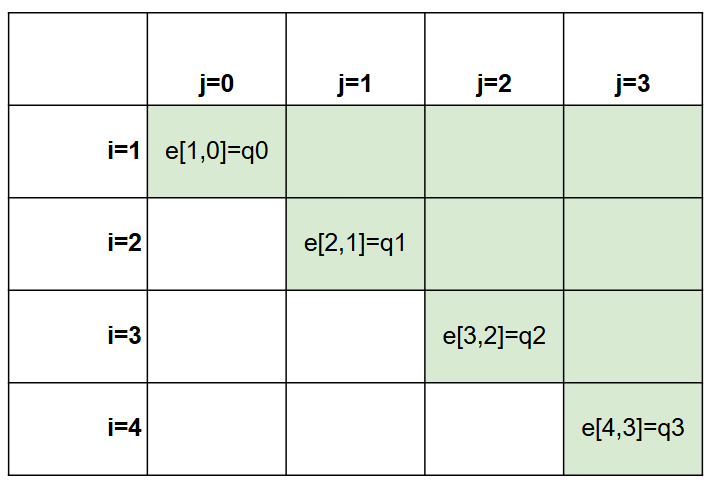
動的計画法アルゴリズムを少し高速化するためにもう一つの表を導入する。

$e[i,j]$ を計算するたびに $w(i,j)$ の値をゼロから計算する代わりに $\Theta(j-i)$ 回の加算を用いて、これらの値を以下の要領で計算して表 $w[1 : n+1, 0 : n]$ に格納する。

ベースケースとして、$1 \le i \le n+1$ に対して $w[i, i-1] = q_{i-1}$ を計算する。$j \ge i$ に対しては、次のように計算する。

$$ w[i, j] = w[i, j-1] + p_j + q_j \tag{14.15} $$

したがって、$\Theta(n^2)$ 個の $w[i,j]$ の値を１個当たり $\Theta(1)$ 時間で計算できる。

OPTIMAL-BST 手続きは、以下の入出力の手続きだ。

  • 入力：
    • 確率 $p_1, \dots, p_n$
    • $q_0, \dots, q_n$
    • サイズ $n$
  • 出力：
    • 表 $e$
    • $\text{root}$

行列連鎖積の MATRIX-CHAIN-ORDER とこの手続きの類似性から、この手続きの動作がわかると思う。

2-4行目の for ループは、$e[i, i-1]$ と $w[i, i-1]$ の値を初期化する。5-14行目の for ループは、漸化式 (14.14) と (14.15) を使用して、$1 \le i \le j \le n$ となるすべての $e[i,j]$ と $w[i,j]$ を計算する。最初の反復で、$l=1$ の場合、for ループは $j=i$ となるすべての $i=1, 2, \dots, n$ について $e[i,i]$ と $w[i,i]$ を計算する。

2回目の反復で、$l=2$ の場合、$j=i+1$ となるすべての $i=1, 2, \dots, n-1$ について $e[i, i+1]$ と $w[i, i+1]$ を計算する、といった具合である。10-14行目の最も内側の for ループは、$k_i, \dots, k_j$ を持つ最適二分探索木の根として使用するキー $k_r$ を決定するために、インデックス $r$ を試す。この for ループは、より良い根が見つかった場合に、$\text{root}[i,j]$ に根として使用するインデックスの現在の値を保存する。

OPTIMAL-BST(p, q, n)
1  e[1:n+1, 0:n], w[1:n+1, 0:n], および root[1:n, 1:n] を新しい表とする
2  for i = 1 to n + 1                                          // 基底段階
3      e[i, i-1] = q_{i-1}                                     // 式 (14.14) より
4      w[i, i-1] = q_{i-1}
5  for l = 1 to n
6      for i = 1 to n - l + 1
7          j = i + l - 1
8          e[i, j] = ∞
9          w[i, j] = w[i, j-1] + p_j + q_j                     // 式 (14.15) より
10         for r = i to j                                      // すべての根 r を試す
11             t = e[i, r-1] + e[r+1, j] + w[i, j]             // 式 (14.14) より
12             if t < e[i, j]                                  // 新たな最小値？
13                 e[i, j] = t
14                 root[i, j] = r
15 return e と root

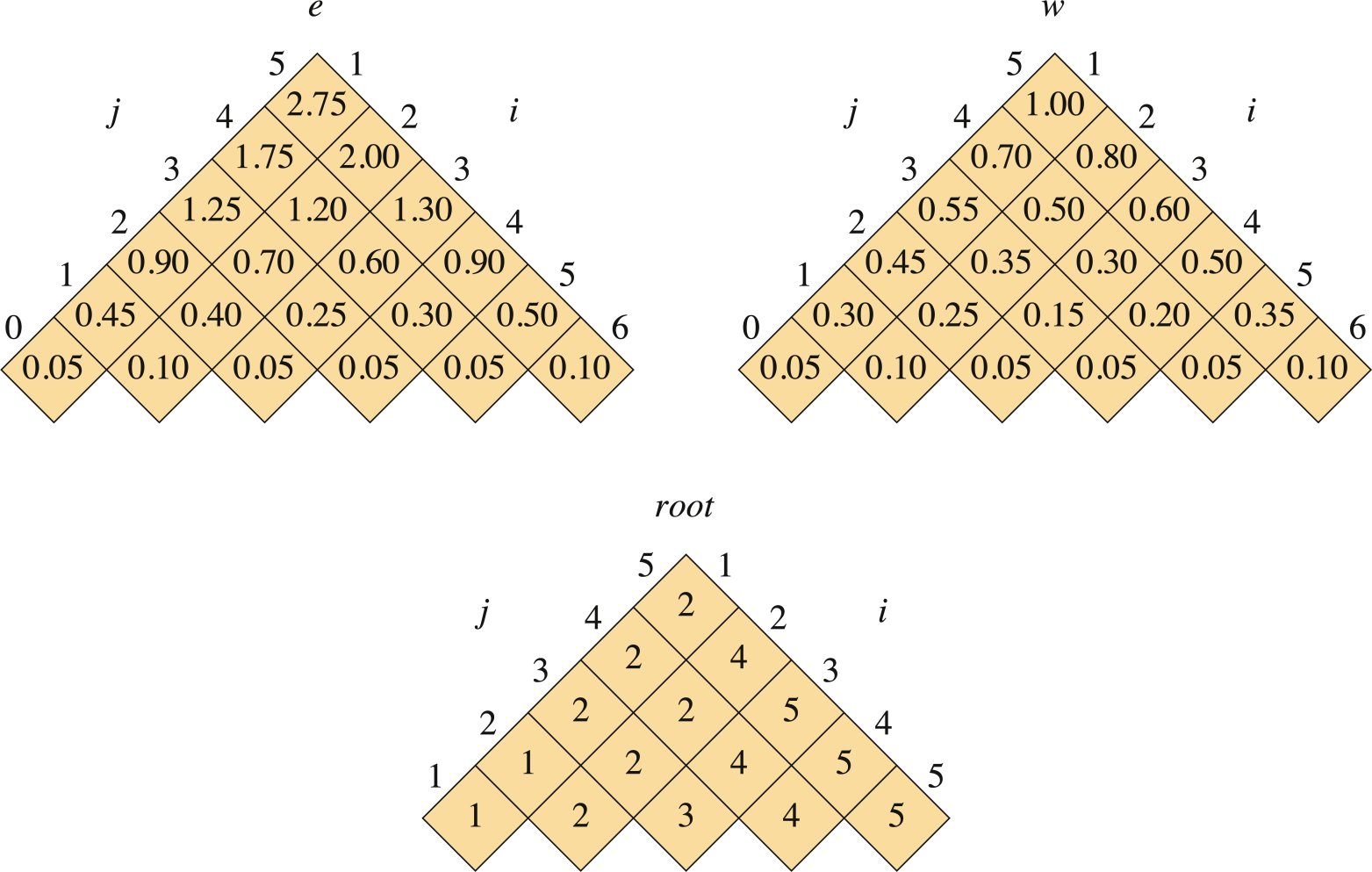
図14.10は、図14.9に示されたキー分布に対して、手続きOPTIMAL-BSTによって計算された表$e[i, j]$、$w[i, j]$、および$root[i, j]$を示している。図14.5の連鎖行列乗算の例と同様に、表は対角線が水平に走るように回転されている。OPTIMAL-BSTは、行を下から上へ、そして各行内では左から右へと計算する。

OPTIMAL-BST手続きは、MATRIX-CHAIN-ORDERと同様に、$\Theta(n^3)$時間かかる。その実行時間は$O(n^3)$である。なぜなら、そのforループは3重にネストされており、各ループインデックスは最大で$n$個の値をとるからである。OPTIMAL-BSTのループインデックスは、MATRIX-CHAIN-ORDERのものとまったく同じ境界を持つわけではないが、すべての方向で最大でも1の範囲内に収まっている。したがって、MATRIX-CHAIN-ORDERと同様に、OPTIMAL-BST手続きは$\Omega(n^3)$時間かかる。

まとめ

具体的な問題を2つ

  • LCS問題
  • 最適二分探索木問題 を取り上げて動的計画法を作る流れを見た。

章末問題

ほんとは具体的な章末問題をいくつか扱いたかったけど、すでに動的計画法の話題だけで分量多くなっているので省略します。