この資料は、アルゴリズム設計・分析の重要なテクニックの一つである動的計画法 (Dynamic Programming, DP) について学ぶことを目的としています。具体的な問題を例に取りながら、その動作原理と適用可能な問題の性質を理解していきます。

ロッド切り出し問題

問題設定の説明

鉄の棒を切り分けて販売する会社を想像してください。この会社は、長い鉄の棒を仕入れ、顧客の需要に合わせて様々な長さに切り出して販売します。長さごとに販売価格が設定されており、どう切り分ければ全体の利益が最大になるかを知りたい、というのが問題です。

ロッド切り出し問題

長さ $n$ インチの棒と $i = 1, 2, \dots, n$ に対する価格表 $p_i$ が与えられたとき、棒を切り出して販売することによって得られる最大収益 $r_n$ を決定せよ。なお、カット自体にコストはかからないものとする。

長さ $i$ $1$ $2$ $3$ $4$ $5$ $6$ $7$ $8$ $9$ $10$
価格 $p_i$ $1$ $5$ $8$ $9$ $10$ $17$ $17$ $20$ $24$ $30$

たとえば、長さ $n=4$ の棒があるとき、この棒を切り分ける方法はいくつか考えられます。

  • まったく切らない（長さ 4 のまま売る）
    • 収益 9
  • 1 と 3 に切る
    • 収益 1 + 8 = 9
  • 2 と 2 に切る
    • 収益 5 + 5 = 10

などなど。以下の図の通り、全部で 8 通りの切り分け方があります。

この場合、最適な切り方は「長さ2の棒2本」であり、その時の最大収益は10です。

長さ n についての最大収入と最適な切り方

Note

もし最適解が棒を $k$ 個の断片に切る場合、ある $1 \le k \le n$ に対して、最適分解は以下のようになる。

$$n = i_1 + i_2 + \dots + i_k$$

長さ $i_1, i_2, \dots, i_k$ の断片への棒の分解は、対応する最大の収益を提供する。

$$r_n = p_{i_1} + p_{i_2} + \dots + p_{i_k}$$

長さ 1 から 10 までの最大収入と最適な切り方を考えてみましょう。

🤔think 🤔deep think 🤔ultra think

【答えの表】

長さ $n$ 最大収益 $r_n$ 最適な分割 (解)
1 1 1 (カットなし)
2 5 2 (カットなし)
3 8 3 (カットなし)
4 10 2 + 2
5 13 2 + 3
6 17 6 (カットなし)
7 18 1 + 6 または 2 + 2 + 3
8 22 2 + 6
9 25 3 + 6
10 30 10 (カットなし)

ではこれを抽象化して、一般の $n\ge1$ に対する最大収入 $r_n$ を $n$ 未満の長さの金属棒に対する最大収入 $r_i\; (1\le i \le n-1)$ を用いて表しましょう。すると以下のようになります。

$$r_n = \max\; (p_n, r_1 + r_{n-1}, r_2 + r_{n-2}, \dots, r_{n-1} + r_1) \tag{14.1}$$

この問題は部分最適構造を持つ

ここで重要な性質に気づきます。長さ $n$ の棒を最適に切り分けた場合、その結果得られる各断片（部分問題）もまた、その長さにおいて最適に切り分けられているはずです。もし、ある断片についてもっと収益が上がる切り分け方があるなら、元の切り分け方も最適ではなかったことになります。

このように、問題全体の最適解が、その部分問題の最適解を含んでいる構造を最適部分構造 (Optimal Substructure) と呼びます。また、各部分問題は互いに影響を与えず、独立して解くことができます。

漸化式の形で最適解を表せる

この「最適部分構造」という性質を利用すると、長さ $n$ の棒の最大収益 $r_n$ を、より短い棒の最大収益を使って表現できます。

最初の1本を長さ $i$ で切り出すと、残りは長さ $n−i$ の棒になります。この長さ $i$ の部分はそのまま売り、残りの $n−i$ の部分は、それ自体で最大収益が得られるように切り分ける（その最大収益は $r_{n−i}$）と考えます。このときの合計収益は $p_i+r_{n−i}$ です。

この最初の切り出し方 $i$ を $1$ から $n$ まで全て試し、その中で最も収益が高くなるものを選べばよいので、以下の漸化式が立てられます。

$$r_n​=\max_{1\le i\le n}​\;(p_i​+r_{n−i​})$$

ただし、$r_0=0$ とします。

ということは、再帰の手続きで最適解を求めるアルゴリズムが作れる

この漸化式を素直にプログラムに落とし込むと、再帰呼び出しを使ったアルゴリズムができます。

CUT-ROD(p, n)
1 if n == 0
2     return 0
3 q = -∞
4 for i = 1 to n
5     q = max(q, p[i] + CUT-ROD(p, n - i))
6 return q

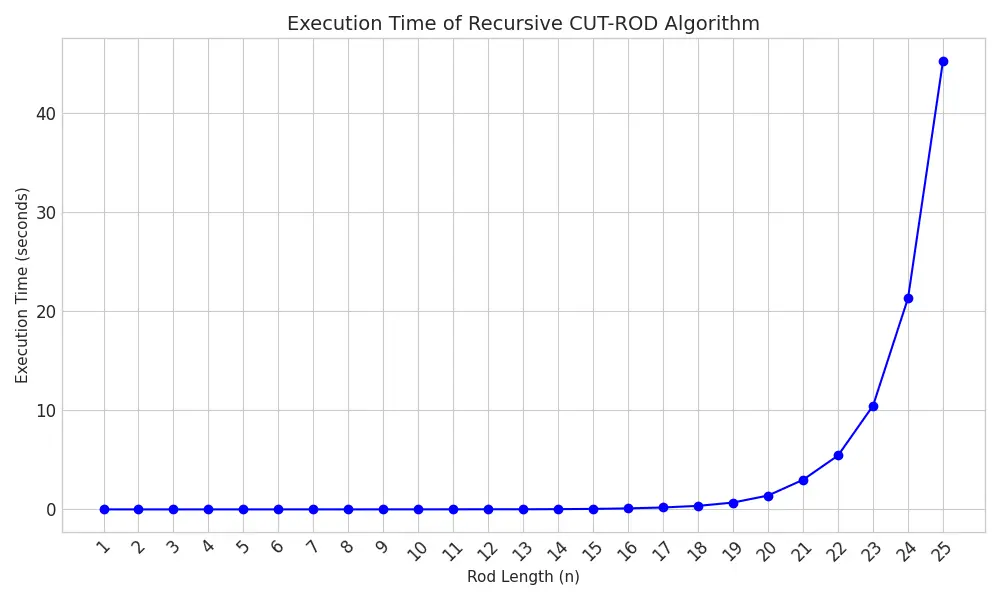
しかし n が大きくなると途端に実行時間が長くなる

この CUT-ROD は、小さな $n$ では問題なく動きますが、$n$ が40程度になるだけで、実行に数分から数時間かかるほど遅くなります。$n$ を1増やすごとに、実行時間がほぼ2倍になる、指数関数的な計算時間 O($2^n$) がかかってしまうのです。

重複している部分が多いのが悪い！

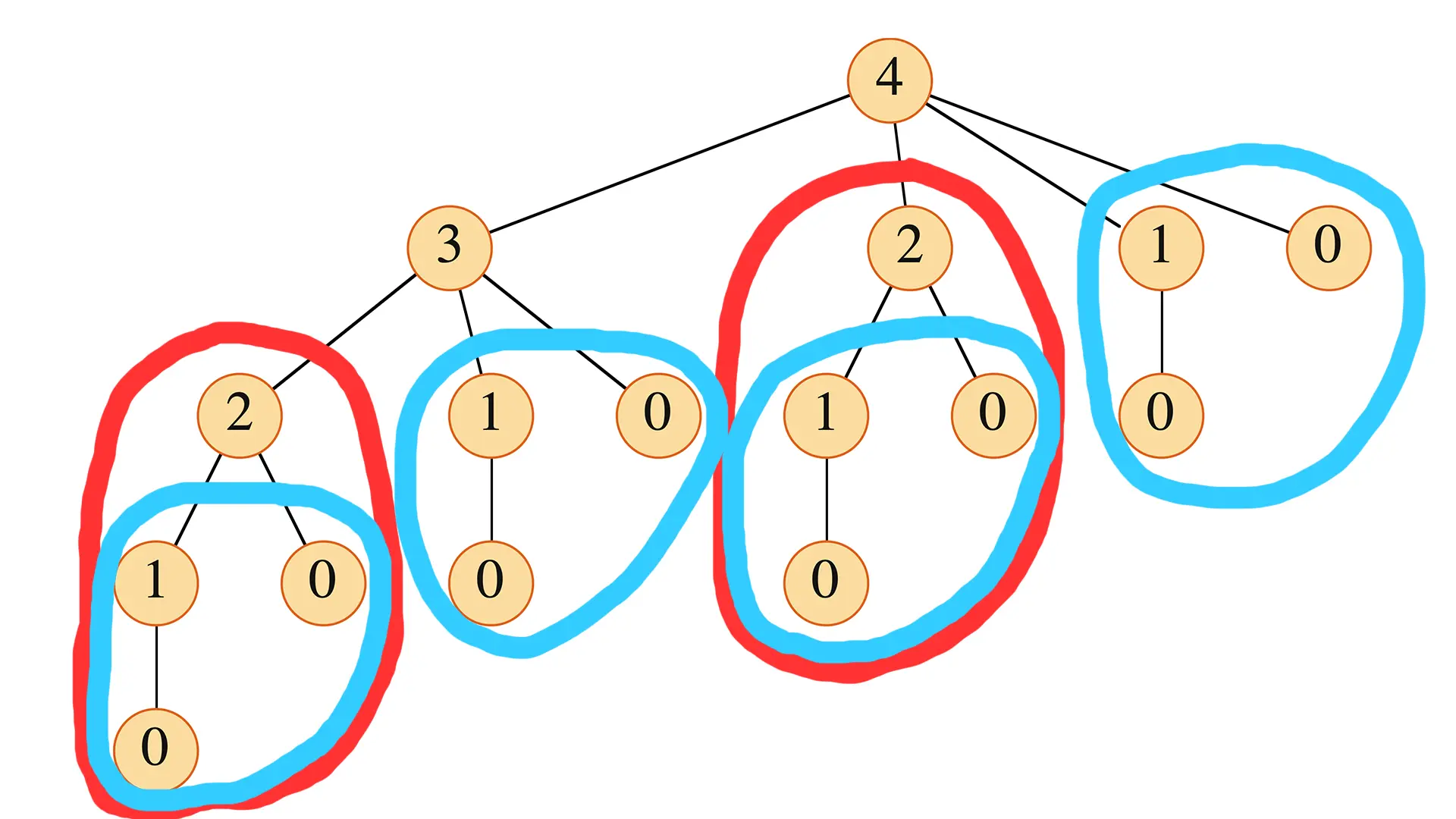
なぜそんなに遅いのでしょうか？$n=4$ の場合の再帰呼び出しの様子を再帰木で見てみましょう。

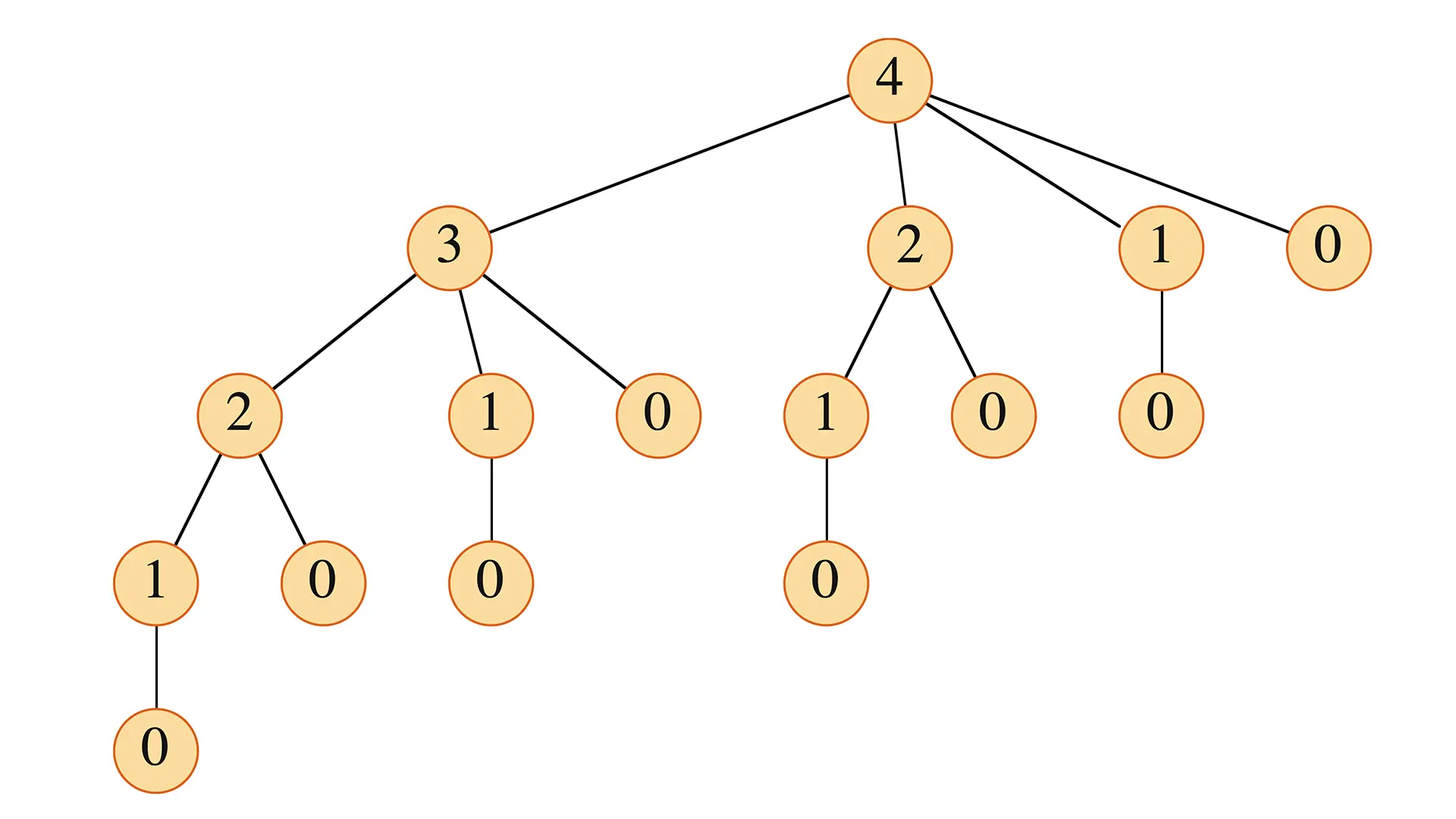
  • CUT-ROD(4) は CUT-ROD(3), CUT-ROD(2), CUT-ROD(1), CUT-ROD(0) を呼び出す
  • CUT-ROD(3) は CUT-ROD(2), CUT-ROD(1), CUT-ROD(0) を呼び出す
  • ……以下同様

この図を見ると、例えば CUT-ROD(2) や CUT-ROD(1) といった同じ計算が、木の異なる場所で何度も何度も繰り返し行われていることがわかります。これが計算時間の爆発的な増大の原因です。

部分問題の答えをメモっとけばよい

この無駄をなくすにはどうすればよいでしょうか？答えは単純です。一度計算した部分問題の答えは、どこかに保存（メモ）しておき、次に同じ計算が必要になったら、再計算せずにメモした値を参照すればよいのです。

履歴管理を用いるトップダウン方式（メモ化再帰）

この「メモ化」のアイデアを、先ほどの再帰アルゴリズムに組み込んでみましょう。この方式をメモ化再帰 (Memorization) またはトップダウン方式と呼びます。

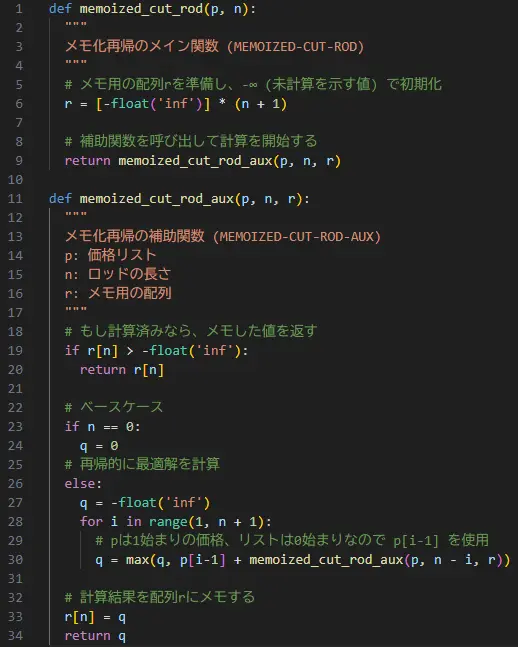
疑似コード: MEMOIZED-CUT-ROD

MEMOIZED-CUT-ROD(p, n)
1 let r[0:n] be a new array // メモ用の配列
2 for i = 0 to n
3     r[i] = -∞
4 return MEMOIZED-CUT-ROD-AUX(p, n, r)

MEMOIZED-CUT-ROD-AUX(p, n, r)
1 if r[n] >= 0         // もし計算済みなら
2     return r[n]      // メモした値を返す
3 if n == 0
4     q = 0
5 else
6     q = -∞
7     for i = 1 to n
8         q = max(q, p[i] + MEMOIZED-CUT-ROD-AUX(p, n - i, r))
9 r[n] = q             // 計算結果をメモする
10 return q

計算時間比較

  • 単純な再帰: 指数時間 $O(2^n)$
  • メモ化再帰: 多項式時間 $\Theta(n^2)$

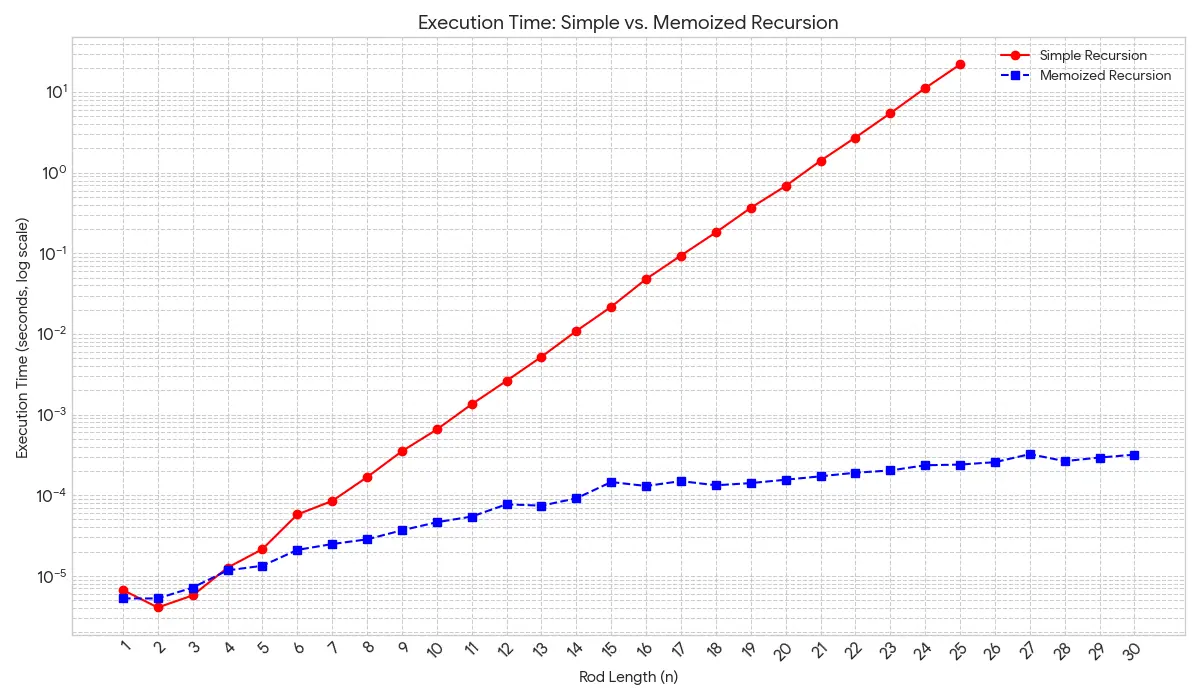
メモ化によって、各部分問題は一度しか計算されなくなり、計算時間が劇的に改善されます。

低次の部分問題はどうせ後で使う

トップダウン方式では、大きな問題から解き始め、必要に応じて小さな部分問題を再帰的に解いていきます。しかし、よく考えると、例えば $r_n$ を計算するためには、結局 $r_0,r_1,\dots,r_{n−1}$ の答えが必要になります。

部分問題の下から計算して保存しておけばいいのでは

それならば、あらかじめ小さい問題から順番に解いていき、その結果をテーブルに蓄えておく方が、再帰呼び出しのオーバーヘッドもなく、よりシンプルで効率的ではないでしょうか？

それが、「ボトムアップ方式」

この考え方に基づくのがボトムアップ方式です。部分問題をサイズの小さい順（$j=0,1,2,\dots,n$）に解き、その結果を配列に保存していきます。

疑似コード: BOTTOM-UP-CUT-ROD

BOTTOM-UP-CUT-ROD(p, n)
1 let r[0:n] be a new array  // 解を保存する配列
2 r[0] = 0
3 for j = 1 to n              // 問題サイズjを小さい順に大きくしていく
4     q = -∞
5     for i = 1 to j
6         q = max(q, p[i] + r[j - i]) // r[j-i]は既に計算済み
7     r[j] = q
8 return r[n]

計算時間比較

  • 単純な再帰: 指数時間 $O(2^n)$
  • メモ化再帰: 多項式時間 $\Theta(n^2)$
  • ボトムアップ: 多項式時間 $\Theta(n^2)$

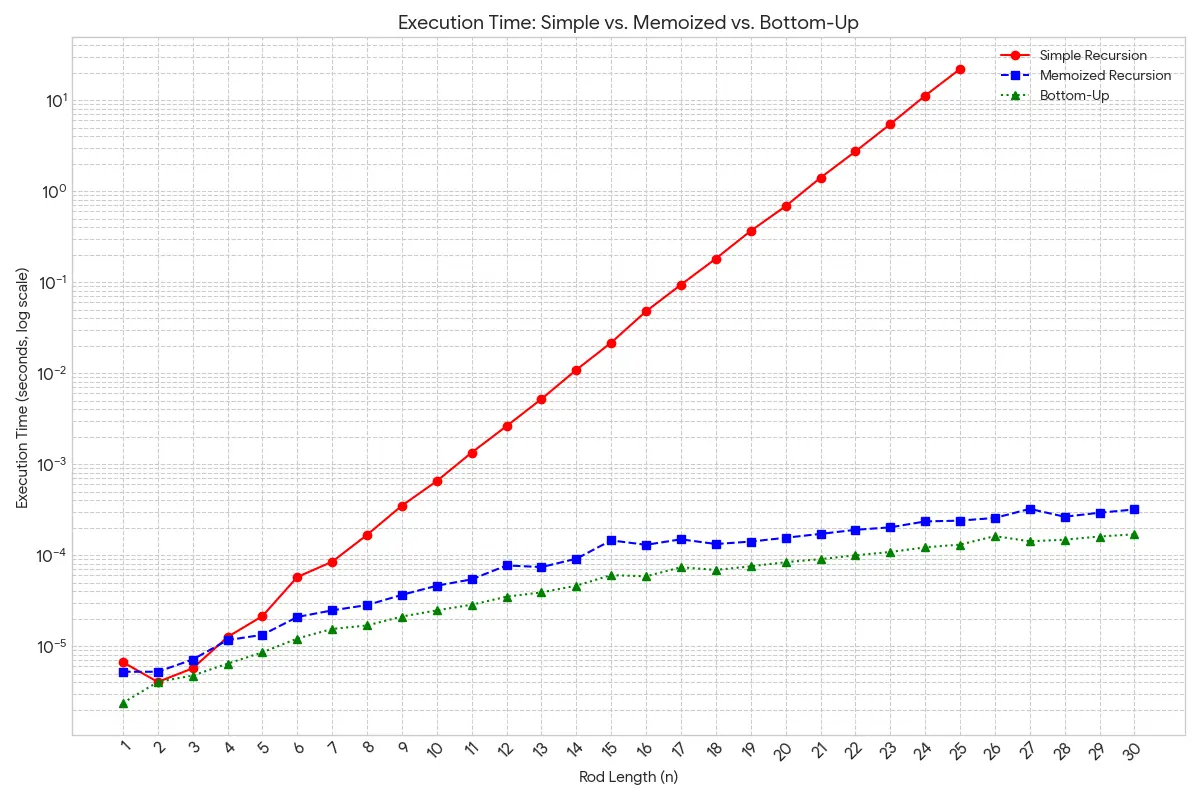
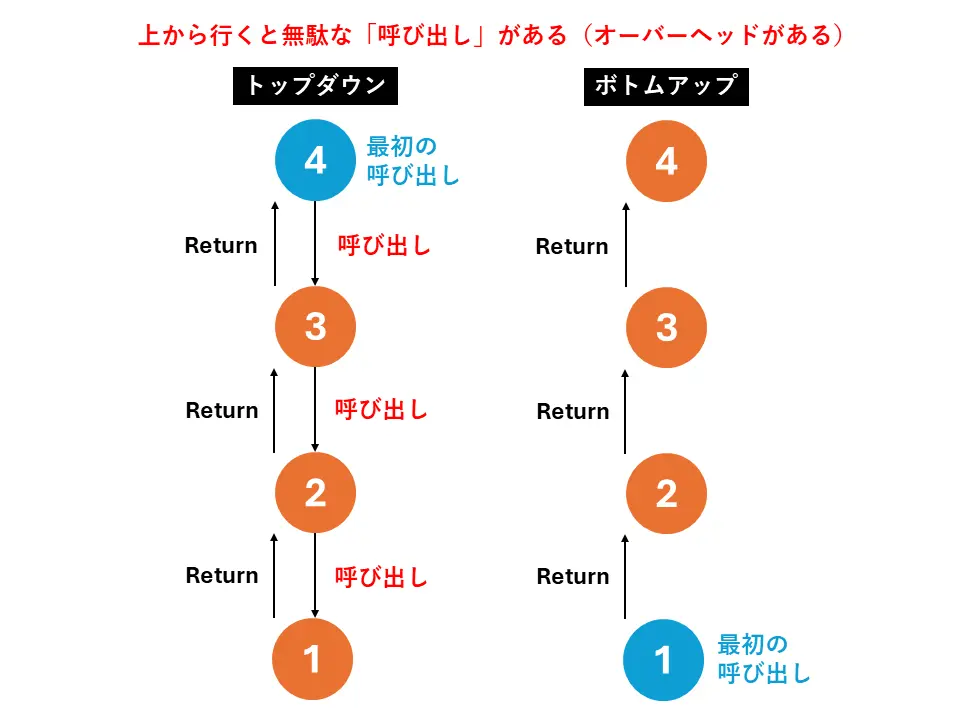
ボトムアップ方式もメモ化再帰と同様に $\Theta(n^2)$ の計算時間で、通常は再帰のオーバーヘッドがない分、定数倍高速に動作します。

オーバーヘッド？

オーバーヘッドとは、ある主要なタスクを遂行するために間接的に必要となる付加的な処理、時間、およびリソース消費を指す包括的な概念のこと。 トップダウン方式だと、上から下に関数呼び出しを連続するのが、その呼び出し回数分オーバーヘッドになっている。

最適な「値」は求められるが、「解」そのものは返さない

ここまで紹介したアルゴリズムは、最大収益（最適値）は求められますが、その収益を達成するための具体的な切り分け方（最適解）は分かりません。

どうしましょう😟

「解」も保存するようにすればいい

解決策は、最適値を計算する際に、「その値を得るためにどの選択をしたか」も一緒に保存しておくことです。ロッド切り出し問題では、「長さ $j$ の棒に対して、最初に切り出すべき最適な長さ $i$」を別の配列 $s$ に記録しておきます。

疑似コード: EXTENDED-BOTTOM-UP-CUT-ROD

EXTENDED-BOTTOM-UP-CUT-ROD(p, n)
1 let r[0:n] and s[1:n] be new arrays
2 r[0] = 0
3 for j = 1 to n
4     q = -∞
5     for i = 1 to j
6         if q < p[i] + r[j - i]
7             q = p[i] + r[j - i]
8             s[j] = i       // 最適な選択肢iを保存
9     r[j] = q
10 return r and s

この $s$ 配列を使えば、以下のようにして解を復元できます。

PRINT-CUT-ROD-SOLUTION(p, n)
1 (r, s) = EXTENDED-BOTTOM-UP-CUT-ROD(p, n)
2 while n > 0
3     print s[n]
4     n = n - s[n]

独立して最適解が求まる＆重複する部分問題を持つようなときは動的計画法が使える

ロッド切り出し問題の経験から、動的計画法が有効な問題には、

動的計画法が有効な問題の2つの特徴

  1. 最適部分構造: 問題の最適解が部分問題の最適解から構成される。
  2. 重複部分問題: 再帰的に解くと、同じ部分問題が何度も出現する。

という2つの性質があることがわかります。

部分問題グラフとしてそれを表現できる

動的計画法における部分問題間の依存関係は、部分問題グラフという有向グラフで表現できます。各ノードが部分問題を表し、部分問題 x の解を求めるのに部分問題 $y$ の解が必要なとき、$x$ から $y$ へ辺を引きます。

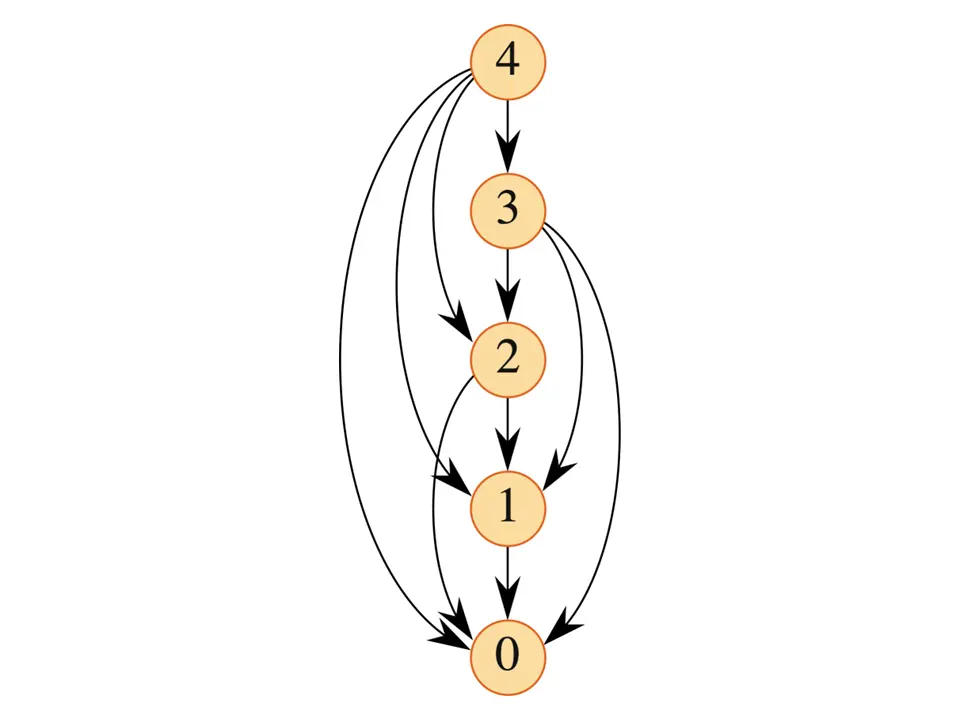
部分問題グラフは、単純な再帰アルゴリズムの再帰木において、重複しているノードを一つにまとめたものと考えることができます。

動的計画法の実行時間は、グラフの頂点数と辺数に比例となることがある

動的計画法の実行時間は、大まかに

$$（部分問題の総数）×（各部分問題を解くための選択肢の数）$$

で決まります。これは部分問題グラフの $（頂点数＋辺数）$ に比例することが多いです。ロッド切り出し問題では、頂点数が $\Theta(n)$、辺数が $\Theta(n^2)$ なので、実行時間も $\Theta(n^2)$ となります。

動的計画法の基本要素

ロッド切り出し問題の例を踏まえて、動的計画法の基本要素を押さえるための質問集を作りました。考えてみましょう。

最適部分構造とは何か？

答え

ある問題に対する最適解が、その部分問題に対する最適解を含んでいる性質のことです。つまり、「大きな問題の最適解」を「小さな問題の最適解」を組み合わせて構築できます。このとき、部分問題同士は互いに干渉しない独立性も重要です。

ロッド切り出しにおける最適部分構造とはどの特性のことを言うのか？

答え

長さ $n$ の棒を最初に長さ $i$ と $n−i$ に切り分けた場合、全体の収益を最大化するためには、残りの長さ $n−i$ の棒もまた、それ自体で収益が最大になるように切り分けられなければならない、という特性が最適部分構造です。

重複性部分問題とは何か？

答え

問題を再帰的に解こうとすると、同じ部分問題が何度も繰り返し解かれる性質のことです。動的計画法は、これらの部分問題の解をメモ化またはテーブル化することで、計算の重複を避け、効率化を図ります。

ロッド切り出しにおける重複性部分問題とはどの特性のことを言うのか？

答え

CUT-ROD(4) を計算する過程で CUT-ROD(2) が複数回呼び出されたように、ある長さの部分問題の計算が、異なる分岐で何度も要求される特性が重複部分問題です。

どうやって動的計画法のアルゴリズムを作るのか？具体的な問題にもどって考えてみよう

これらの要素を念頭に、もう一つ別の具体的な問題を通して、動的計画法のアルゴリズム設計プロセスを体験してみましょう。

連鎖行列乗算問題

問題設定の説明

複数の行列の積 $A_1 A_2 \cdots A_n$ を計算する問題を考えます。行列の積は結合法則が成り立つので、計算する順番（括弧の付け方）を変えても結果は同じです。

ただここで重要なのは、計算する順番によって、必要となるスカラー乗算の回数が劇的に変わることがある、ということです。

たとえば、$A_1(10行\times100列), A_2(100行\times5列), A_3(5行\times50列)$ という3つの行列の積を考えます。

  • $((A_1A_2)A_3)$ の順で計算：
    • $A_1A_2: 10\times100\times5=5,000$ 回
    • $(A_1A_2)A_3: 10\times5\times50=2,500$ 回
    • 合計: 7,500 回
  • $(A_1(A_2A_3))$ の順で計算：
    • $A_2A_3: 100\times5\times50=25,000$ 回
    • $A_1(A_2A_3): 10\times100\times50=50,000$ 回
    • 合計: 75,000 回

このように、計算順序を変えるだけで、計算コストが10倍も変わります。

連鎖行列乗算問題は、このスカラー乗算の回数が最小になるような、最適な括弧の付け方（計算順序）を見つける問題です。

まずは単純にしらみつぶしに数え上げようとするとどうなるか？

ものごとはなるべく単純な方が良いので、まずは全ての括弧の付け方を試す 「しらみつぶし（総当たり）」 だとどうなるかを考えみましょう。

$n$ 個の行列の括弧の付け方の総数 $P(n)$ は、以下の漸化式で表されます。

$$P(n)=\begin{cases} 1 \quad &\text{(if $n=1$のとき)}\\ \displaystyle\sum_{k=1}^{n−1}​P(k)P(n−k) \quad &\text{(if $n\ge 2$のとき)} \end{cases}$$

この解はカタラン数として知られており、$\Omega(4^n/n^{3/2})$ という爆発的な速さで増加します。したがって、総当たりは現実的ではありません。

カタラン数が出てくるほかの事象

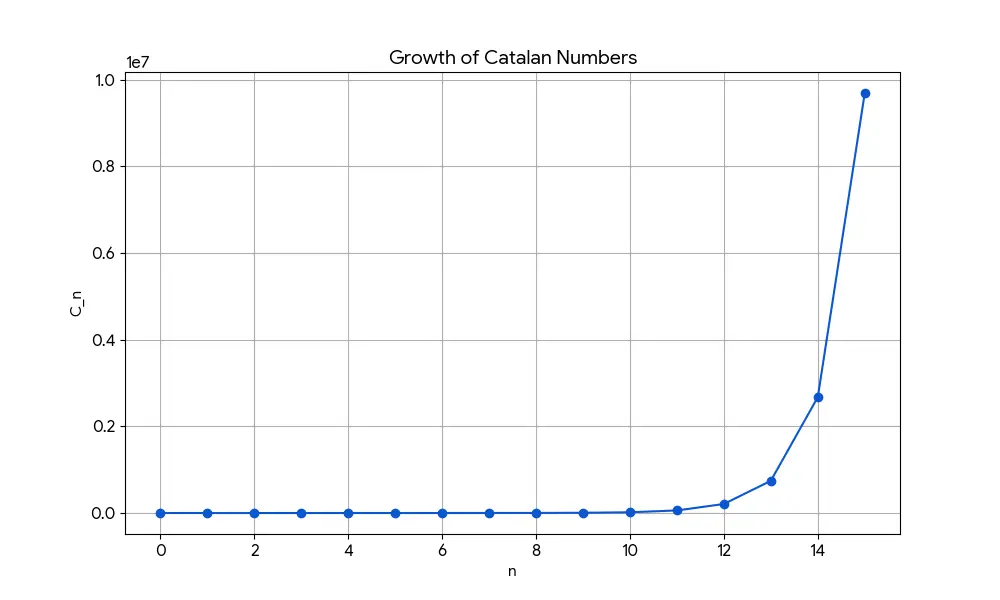
  • 二分木 : $C_n$ は、$n$ 個の分岐を持つ（ $n+1$ 枚の葉を持つ）二分木の総数である。以下の図は $C_3 = 5$ の場合である。

  • 格子状の経路数え上げ : $C_n$ は、縦横 $n$ マスずつの格子において、次の図のように対角線を跨がずに格子点を通って、向かい合った点を最短距離で繋ぐ道順の総数と説明できる。以下の図は $C_4 = 14$ の場合である。

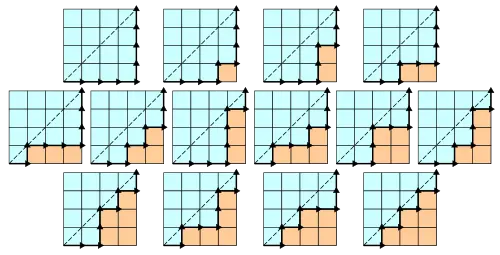
  • 多角形の三角形分割 : $n+2$ 個の辺からなる凸多角形を、頂点どうしを結ぶ線を互いに交差しないように引いて、$n$ 個の三角形に切り分けることを考える。この分け方の場合の数は、カタラン数 $C_n$ である。以下の図は $n=4$ の場合である。

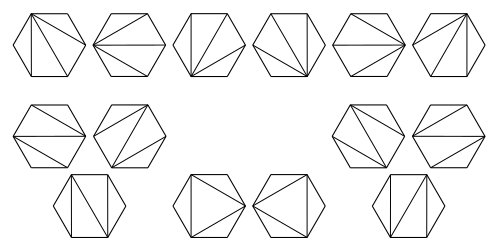
うまい方法はないだろうか？

動的計画法がうまいこといくかどうかを調べるために部分最適構造と重複性部分問題について考えてみよう。

  1. 最適部分構造: 積 $A_i\cdots A_j$ を最適に計算する際、最後の分割が $A_k$ と $A_{k+1}$ の間で行われるとします。このとき、部分積 $(A_i\cdots A_k)$ と $(A_{k+1}\cdots A_j)$ もまた、それぞれが最適に計算されていなければなりません。これは最適部分構造を持つことを示唆しています。
  2. 重複部分問題: $(A_1\cdots A_n)$ を考える過程で、部分問題 $(A_i\cdots A_j)$ が何度も計算対象として現れます。これもDPの適用を後押しします。

部分問題の最適解を使って再帰的にもとの問題の最適解のコストを計算しよう

最適部分構造があるため、ロッド切り出し問題と同様に、最適コストを漸化式で表現できます。行列の連鎖 $A_i\dots A_j$ を計算する最小コストを $m[i,j]$ とすると、

$$ m[i,j]= \begin{cases} 0 \quad &(i=j) \\ \displaystyle{\min_{i \le k\lt j} ​\{ m[i,k] + m[k+1,j]+p_{i−1​}p_k​ p_j​ \}} ​\quad &(i\lt j) \end{cases}$$

ここで $p_{i−1}\times p_i$ は行列 $A_i$ のサイズです。この漸化式をボトムアップ方式で解くことで、効率的に最適値を計算できます。

ボトムアップで実装

この漸化式をボトムアップで実装したアルゴリズムが MATRIX-CHAIN-ORDER です。短い連鎖から順に計算コストをテーブルに埋めていきます。

疑似コード: MATRIX-CHAIN-ORDER

MATRIX-CHAIN-ORDER(p, n)
 1 let m[1..n, 1..n] and s[1..n-1, 2..n] be new tables
 2 for i = 1 to n
 3     m[i, i] = 0
 4 for l = 2 to n                          // l は連鎖長
 5     for i = 1 to n - l + 1
 6         j = i + l - 1
 7         m[i, j] = ∞
 8         for k = i to j - 1              // 分割位置kを試す
 9             q = m[i, k] + m[k + 1, j] + p[i-1]*p[k]*p[j]
10             if q < m[i, j]
11                 m[i, j] = q
12                 s[i, j] = k             // 最適な分割位置を保存
13 return m and s

計算時間比較

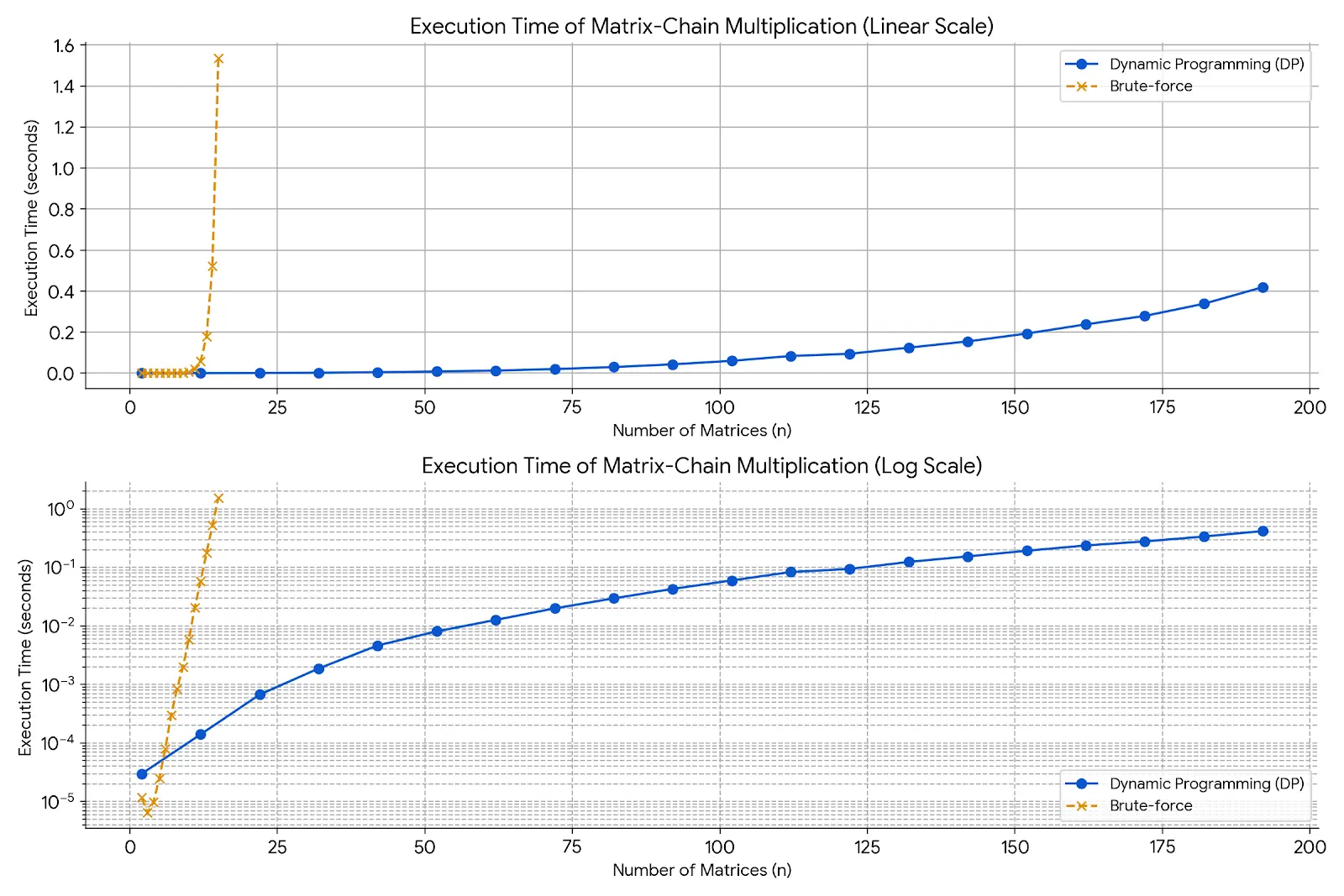
  • 総当たり: 指数時間 $\Omega(4^n/n^{3/2})$
  • 動的計画法: 多項式時間 $\Theta(n^3)$

最適解の再構成

ロッド切り出し問題と同様に、最適コストを計算する際に、どの $k$ で分割したときに最小コストが得られたかをテーブル $s$ に保存しておきます。この $s$ テーブルを再帰的にたどることで、最適な括弧の付け方を復元することができます。

手続き MTRIX-CHAIN-ORDER で計算した表 $m$ と $s$ の図。ただし $n = 6$ であり、各行列の次元は次の表で与えられるものとする。

行列 $A_1$ $A_2$ $A_3$ $A_4$ $A_5$ $A_6$
次元 $30\times 35$ $35\times 15$ $15\times 5$ $5\times 10$ $10\times 20$ $20\times 25$

今回のまとめ

最後に、動的計画法について学んだことをまとめます。

■ 動的計画法の適用できる問題の2つの特徴

動的計画法は、以下の2つの性質を持つ最適化問題に有効な手法です。

  • 最適部分構造 (Optimal Substructure)
    • 問題の最適解が、その部分問題の最適解から構成される。
  • 重複部分問題 (Overlapping Subproblems)
    • 単純な再帰で解くと、同じ部分問題が何度も出現する。

■ アルゴリズムの作り方

動的計画法のアルゴリズムは、一般的に以下の4ステップで設計されます。

  1. 最適解の構造を特徴付ける: 最適部分構造を見つけ出す。
  2. 最適解の値を再帰的に定義する: 漸化式を立てる。
  3. 最適解の値を計算する: ボトムアップまたはトップダウン（メモ化）で漸化式を計算する。
  4. 最適解を構築する: 計算過程で保存した情報から、実際の解を復元する。

■ ２種類のパターン

計算の実行方法には、主に2つの同等なアプローチがあります。

  • トップダウン方式
    • 再帰的な構造を保ちつつ、計算結果をメモして重複計算を避ける。
  • ボトムアップ方式
    • 小さい部分問題から順に解き、結果をテーブルに蓄積していく。